九年级上341相似三角形的判定（1)VIP免费

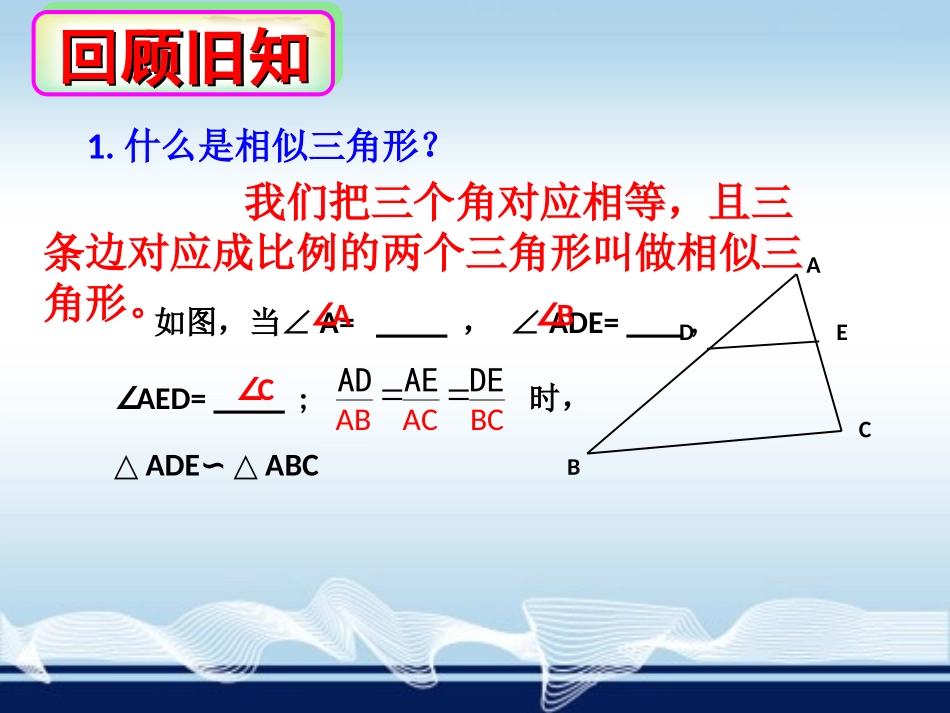
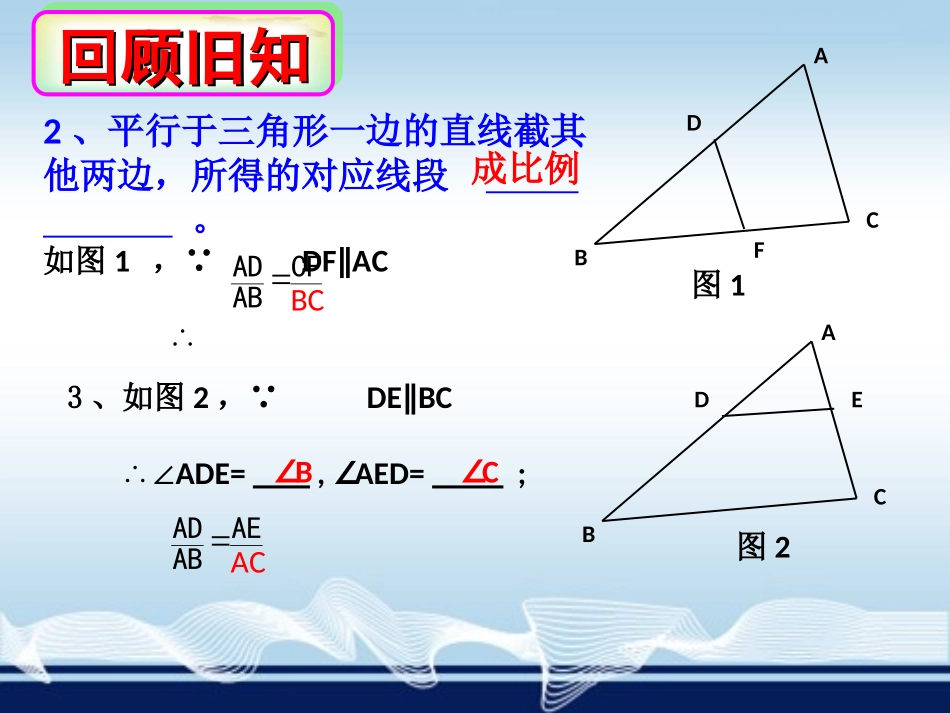
义务教育教科书数学九年级上册3.4.1相似三角形的判定（1）杨镇中学周华锋1.什么是相似三角形？我们把三个角对应相等，且三条边对应成比例的两个三角形叫做相似三角形。ABCDE如图，当∠A=，∠ADE=,∠AED=;时，△ADEABC∽△DEAEAD∠A∠B∠CABACBC回顾旧知回顾旧知回顾旧知回顾旧知ABCDF图12、平行于三角形一边的直线截其他两边，所得的对应线段。如图1，∵DFAC∥∴成比例CFABADABCDE3、如图2，∵DEBC∥∴∠ADE=,∠AED=;AEABAD图2∠B∠CACBC回顾旧知回顾旧知回顾旧知回顾旧知P77“动脑筋”AD=AB=AC=DE=BC=AE=cmcmcmcmcmcm1.32.82.61.81.40.9BCDEACAEABAD所以△ADEABC∽△探究探究如图3-14，在△ABC中，D为AB上任意一点，过点D作BC的平行线DE，交AC于点E。(1)ADE△与△ABC的三个角分别相等吗？在△ADE和△ABC中，∠A=∠A∵DEBC∥∴∠ADE=∠B,∠AED=∠C;(2)分别度量△ADE与△ABC的边长，他们的边长是否对应成比例？（3）△ADE与△ABC有什么关系？学习新知学习新知学习新知学习新知如图，在△ABC中，D为AB上任意一点，过点D作BC的平行线DE，交AC于点E。求证：△ADE∽ABC△。ABCDE证明：在△ADE和△ABC中，∠A=∠A∵DEBC∥∴∠ADE=∠B,∠AED=∠C;AEABADAC过点D作DF∥AC，交BC于点F。∵DFAC∥∴CFABADBC∵四边形DFCE为平行四边形∴DE=CF∴△ADEABC∽△∴DEAEADABACBCF当∠A=,∠ADE=,∠AED=;时，△ADEABC∽△∠B∠C∠ABCCFACAEABAD∴ABCDF图12、平行于三角形一边的直线截其他两边，所得的对应线段。如图1，∵DFAC∥∴成比例ABCDE3、如图2，∵DEBC∥∴图2AEABADACCFABADBCAEABADACBCCF回顾旧知回顾旧知回顾旧知回顾旧知结论结论平行于三角形一边的直线与其他两边相交，截得的三角形与原三角形相似。如图2，如果DEBC∥，那么△ADEACB∽△。你能证明吗？DEACB图2ABCDE图1例题例题例1如图，在△ABC中，已知D，E分别是AB，AC边的中点.求证：△ADE∽△ABC.证明∵点D，E分别是AB，AC边的中点，∴DE∥BC.∴△ADE∽△ABC.例题例题例2如图，点D为△ABC的边AB的中点，过点D作DE∥BC，交边AC于点E.延长DE至点F，使DE=EF.求证：△CFE∽△ABC.证明∵DE∥BC，点D为△ABC的边AB的中点，∴AE=CE.∴△ADE∽△ABC.又DE=FE，∠AED=∠CEF，∴△ADE≌△CEF.∵DE∥BC，∴△CFE∽△ABC.跟踪练习跟踪练习1.如图，在Rt△ABC中，∠C=90°.正方形EFCD的三个顶点E，F，D分别在边AB，BC，AC上.已知AC=7.5，BC=5，求正方形的边长.解：∵四边形EFCD是正方形，∴EDBC,ED=DC=FC=EF.∥AEDABC.ADEDACBC=.7.57.55ACDCEDDCDCACBC=,即=.3DE，即正方形的边长为3.跟踪练习跟踪练习2.如图，已知点O在四边形ABCD的对角线AC上，OE∥BC，OF∥CD.试判断四边形AEOF与四边形ABCD是否相似，并说明理由.解：∵OE∥BC，OF∥CD，∴∠AEO=ABC,AOE=ACB,AOF=ACD,AFO=ADC.∠∠∠∠∠∠∠∴∠AOE+AOF=ACB+ACD,∠∠∠即∠EOF=BCD.∠又∵OE∥BC，OF∥CD，∴△AOE~ACB,AOF~ACD.△△AEEDAOOFADABBCACCDDC====.∴四边形AEOF与四边形ABCD相似.