简单的三角恒等变换二VIP免费

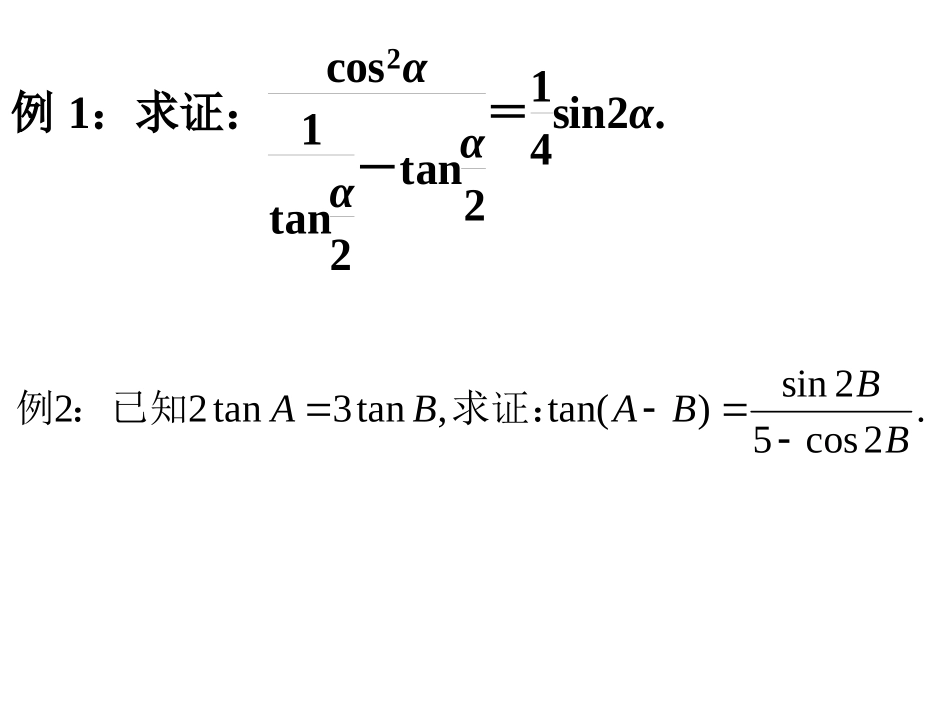
简单的三角恒等变换（第二课时）例1：求值(1)cos10°tan20°＋3sin10°tan70°－2cos40°(2))10tan31(50sin00.2cos52sin)tan(,tan3tan22BBBABA求证：：已知例例1：求证：cos2α1tanα2－tanα2＝14sin2α.：21(1)sinαcosβ=[sin(α+β)+sin(α-β)]2θ+φθ-φ(2)sinθ+sinφ=2sincos22例求证：证明：(1)∵sin(α+β)=sinαcosβ+cosαsinβsin(α-β)=sinαcosβ-cosαsinβ将上两式相加得sin(α+β)+sin(α-β)=2sinαcosβ1sinαcosβ=[sin(α+β)+sin(α-β)]2即例3：积化和差公式：1sinαcosβ=[sin(α+β)+sin(α-β)]21cosαsinβ=[sin(α+β)-sin(α-β)]21cosαcosβ=[cos(α+β)+cos(α-β)]21sinαsinβ=[cos(α+β)-cos(α-β)]2练习：P142，练习2_____tantan,42cos52cos3)2_______tantan,53)cos(,51)cos()122BACBAABC则中，若在若练习：(2)sin(α+β)+sin(α-β)=2sinαcosβ，，α+β=θα-β=φ设θ+φθ-φα=β=22，。那么、αβ把的值代入上式得θ+φθ-φsinθ+sinφ=2sincos22。和差化积公式：α+βα-βsinα+sinβ=2sincos22α+βα-βsinα-sinβ=2cossin22α+βα-βcosα+cosβ=2coscos22α+βα-βcosα-cosβ=-2sinsin22练习：P142，练习3的最小正周期、最值。探究：函数xxycos3sinxbxaycossin)sin(xAy转化abxbaxbxaytan),sin(cossin22其中辅助角公式：xxxfAxAxf2cos)62sin()()1(2||,0,0)sin()(2）其中（，如：经下列函数化简成形例21sin2sin21)()2(2xxxf不同角化成同角2122cos12sin21)(xxxf)2cos2(sin21xx)42(sin22x降幂：二倍角公式合并：降名：辅助角公式1cossin32sincos)()3(22xxxxxf)4sin()4sin(32cossin2)()4(xxxxxf)2sin3,(cos),),4cos(22(,)(3xxbmxabaxf其中向量：已知函数例的值。，求实数的最大值为若函数mxf15)(的值。求若的值求的最小正周期：已知函数例00022cos],8,8[,2523)2()2()1(2)0,(1cossin2cos2)(4xxxfRxxxxxf的最小值。个零点，求上至少有在区间的图像，若个单位，得到函数下移动个单位，再向的图像向右平移将bbxgxgxf10],0[)()(18)()3(本节课小结：xbxaycossin)sin(xAy转化同角常用方法：降幂，合并，降名