高一数学正切函数的图象和性质课件VIP免费

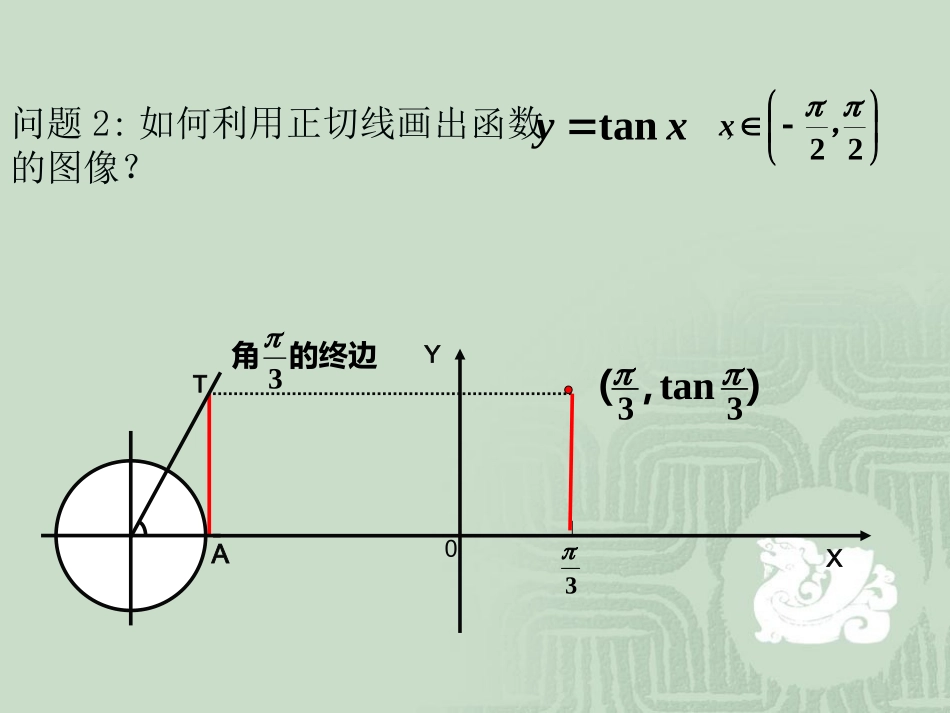
如何用正弦线作正弦函数图象呢？用正切线作正切函数y=tanx的图象.]2,0[,sin1图象、用平移正弦线得xxy.2图象向左、右扩展得到、再利用周期性把该段类比∴是周期函数，是它的一个周期．y=tanx我们先来作一个周期内的图象。∵fx+π=tanx+π=tanxxf用正切线作正切函数图象?2,tan是否为周期函数正切函数kxxy问题1：观察正切线ππ(-,)223），（33tanAT0XY问题2:如何利用正切线画出函数,的图像？xytan22，x的终边角3作法:(1)等分：(2)作正切线(3)平移(4)连线把单位圆右半圆分成8等份。83488483，，，，，利用正切线画出函数，的图像:xytan22，x44288838320oxy由正切函数的周期性，把图象向左、向右扩展，得到正切函数的图象，称为正切曲线yx1-1/2-/23/2-3/2-0y=tanx从图中可以看出,正切曲线是由被相互平行的直线)(,2Zkkx所隔的无穷多支曲线组成的.(1)正切函数是整个定义域整个定义域上的增函数吗？为什么？思考：在每一个开区间，内都是增函数。ππ(-+kπ,+kπ)22kZAB(2)正切函数会不会在某一区间内是减函数？为什么？总结：正切函数的性质：tanyx定义域：{|,}2xxkkZ值域：R周期性：正切函数是周期函数，周期是奇偶性：奇函数单调性：在(,)22kkkZ内是增函数xy22o22tanyx对称性：对称中心是(,0),2kkZ对称轴呢AB求下列函数的定义域xytan11)2(例1：求函数y=tan(x+/4)的定义域xytan)1(变式：,().232xxkkZ解：函数的自变量应满足12,.3xkkZ即12,.3xxkkZ所以，函数的定义域是()tan()2323xx由于f(x)=tantan2)(2),23xfx=（因此函数的周期是251,.22,223233kxkkZkxkkZ由-解得.32tan区间的定义域、周期和单调求函数xy例2：Zkkk,231235），（函数的单调递增区间为.32tan区间的定义域、周期和单调求函数xy,()232xxkkZ函数的自变量应满足552263xkxk)tan(),23xx设f(则tan()tan()tan2)232323xxx（f(x)=f(x+2)函数的周期为215,()2223233kxkkZkxk由得2523xxkkZ所以函数的定义域是，152()33xkkkZ因此，函数的单调递减区间是（2，），解：）（）（由于32tan32tanxx变式：交点间的距离是多少？的相邻两支的与为常数直线xyaaytan)(解：由图象间隔是多少？距离为例3、（1）正切函数的图像：（2）正切函数的性质：定义域：值域：周期性：奇偶性：单调性:对称性：Zkkxx,2|全体实数R正切函数是周期函数，最小正周期T=奇函数正切函数在开区间内都是增函数。Zkkk,2,2对称中心是(,0),2kkZ（3）本课应用数形结合、类比、归纳、化归等数学思想方法