二次根式的加减法课件VIP免费

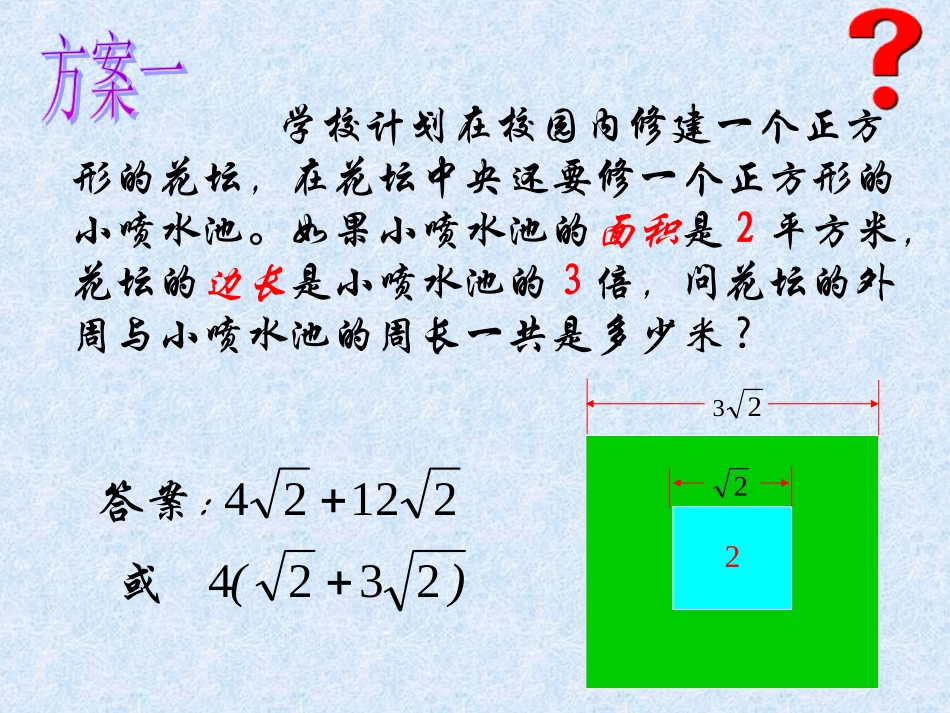
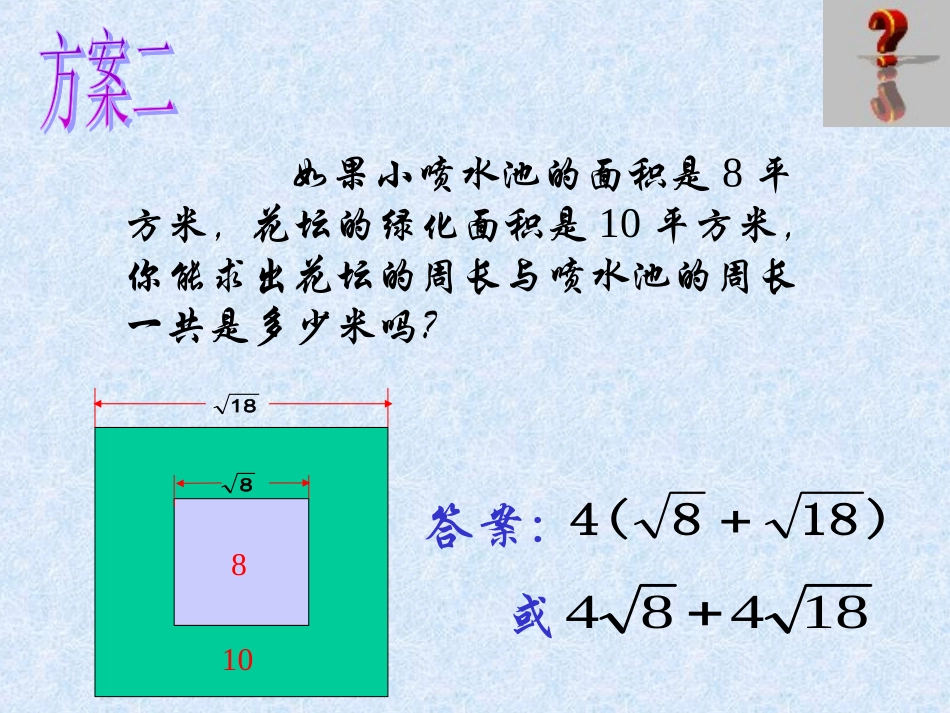
学校计划在校园内修建一个正方形的花坛，在花坛中央还要修一个正方形的小喷水池。如果小喷水池的面积是2平方米，花坛的边长是小喷水池的3倍，问花坛的外周与小喷水池的周长一共是多少米?)(232421224或:答案2232如果小喷水池的面积是8平方米，花坛的绿化面积是10平方米，你能求出花坛的周长与喷水池的周长一共是多少米吗？答案：18484)1884(或810188•二次根式加减运算的基本方法•结论1:如果几个二次根式是同类二次根式，那么可直接根据分配律进行加减运算。•结论2:如果所给的二次根式不是最简二次根式,应该先化简，再考虑进行加减运算。212242)124(216…………(分配律)18484212282)128(……………..(化简)……………..(分配律)2201.被开方数中不含开得尽方的因数或因式；2.被开方数不含分母。复习回顾复习回顾判断同类二次根式的关键是什么？(1)化成最简二次根式；(2)被开方数相同,根指数都等于2。复习回顾复习回顾判断一组式子是否为同类二次根式，与最简二次根式前面的因式及符号无关．比较二次根式的加减与整式的加减，你能得出什么结论？二次根式的加减实质是合并同类二次根式．整式的加减的实质是合并同类项．尝试计算：535211882)1625(93aaa（3）合并同类二次根式。一化二找三合并二次根式加减法的步骤：（1）将每个二次根式化为最简二次根式；（2）找出其中的同类二次根式；交流归纳交流归纳3123234314解：原式基础探究：计算：483316122.1（合并同类二次根式：系数相加减，根指数及被开方数不变）(化简)3)1224(解：原式=532012.232533基础探究：计算：注意:不是同类二次根式的二次根式.(如与)不能合并.523535（化简、去括号）（合并）解：原式=基础探究：计算：xxxx1246932.3x3x2x3x2（化简）（合并）1.判断:下列计算是否正确?为什么?;53215329421883（×）（×）（×）;22222练习一：(1)188(2)75271(3)4863(4)23.4554C下列计算正确的是（）A.5.83211231.22BDaaa23836Ｄ22052189827135)(6)811(4)323100.084832练习计算：（1）80（）（）（）(240.5333210241633326435.23(23).45552051422.7112xxBaxbxabxCabDab练习下列计算正确的是（）A.2xB应用探究：22448170xyxy22321(9)(5)3xyxxyxxyxx已知，求的值．1.如何合并同类二次根式?合并同类二次根式与合并同类项类似，把根号外系数或字母相加减,根指数和被开方数不变.先把不是最简二次根式的化为最简二次根式,再找出同类二次根式，最后把同类二次根式分别合并.（一化二找三合并）.2.二次根式加减运算的步骤?思考题：•已知，求的值.6,8xyxyyxxyxy把下列各式化为最简二次根式：（1）（2）（3）211883127baba3123解得：221212318228（1)331313327（2)abbbaababa13（3)观察：以上三组二次根式化简后，被开方数有何特征？你能归纳出同类二次根式的定义吗？同类二次根式:几个二次根式化成___________以后，如果_______相同，这几个二次根式就叫做同类二次根式。最简二次根式被开方数比一比：同类二次根式与同类项的异同。•同类项：所含字母相同，相同字母的次数也相同。•联系：都含“同类”两字，都具有某种共同的性质。都有“相同”两字。•区别：同类项不带根号，同类二次根式有根号。1、判断下列各组二次根式是否为同类二次根式?（1）（）（2）（）（3）（）5.050与1812与aa13与是否是3D31C6B3A2xxDxCxBxA661668.1317227DCBA323312aaDxxCaaaBxyxyA与与与与（4）下列各组式子中是同类二次根式的一组是（）（1）下列根式中，与为同类二次根式的是（）（2）下列根式中与不是同类二次根式的是（）（3）下列根式中，与为同类二次根式的是（）32x6182、选择题CDBB判断几个二次根式是同类二次根式的方法:一是化每个二次根式为最简二次根式；二是看化简后的二次根式中被开方数是否相同。babab26,32,3,271,501,75,283下列各式中哪些是同类二次...