相似三角形的判定上课VIP免费

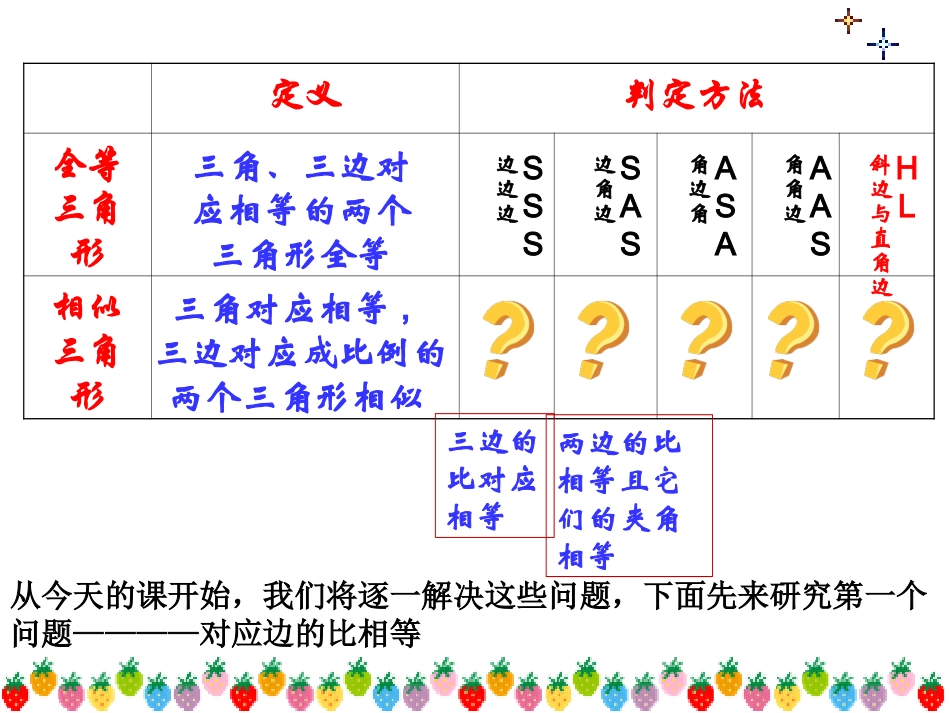
1.学习过哪些判定三角形相似的方法？一、复习回顾定义法：三角对应相等,三边对应成比例的两个三角形相似平行法：平行于三角形一边的直线和其他两边相交，所构成的三角形与原三角形相似2、全等三角形与相似三角形有怎样的关系？3、两个三角形全等有哪些常用的判定方法？全等是相似的特殊情况ADABDEBC，∥练习：如图，ABCADE∽BCDEEDCBAACAE定义判定方法全等三角形相似三角形三角、三边对应相等的两个三角形全等三角对应相等,三边对应成比例的两个三角形相似角边角ASA角角边AAS边边边SSS边角边SAS斜边与直角边HL三边的比对应相等两边的比相等且它们的夹角相等从今天的课开始，我们将逐一解决这些问题，下面先来研究第一个问题————对应边的比相等任意画一个三角形，再画一个三角形，使它的各边长都是原来三角形各边长的k倍，度量这两个三角形的对应角，它们相等吗？这两个三角形相似吗？例如：画一个三角形使边长为：6cm、7cm、4cm，再画一个三角形，使它的各边长都是这个三角形各边长的2倍或倍。（单数排画2倍，双数排画倍）1212边边边SSS请将画好的三角形剪下来，比较他们的对应角相等吗？这两个三角形相似吗？小组讨论，由此你得到什么规律及结论？BCAA`B`C`命题：如果两个三角形的三组对应边的比相等，那么这两个三角形相似。BCAA`B`C`已知:如图△ABC和△A`B`C`中kCAACCBBCBAAB''''''求证:ABCA`B`C`△∽△结合命题和图形，说出已知和求证？在线段A’B’上截取A’D=AB过点D作DEB’C’∥，交A’C’于点E.已知:如图△ABC和△A’B’C’中求证:ABCA’B’C’△∽△''''''ABBCACkABBCAC证明：△A’DEA’B’C’∽△''''''''ADDEAEABBCAC''''''ABBCACABBCAC A’D=AB同理：DE=BCA’E=AC△A’DEABC≌△△ABCA’B’C’∽△'''''AEACACAC∴A’B’C’ABCDE如果两个三角形的三组对应边的比相等，那么这两个三角形相似。（SSS）BCAA`B`C`几何语言描述：kCBBCCAACBAAB``````∴△ABCA`B`C`∽△相似三角形判定定理1：简称：三边对应成比例，两三角形相似。定义判定方法全等三角形相似三角形三角、三边对应相等的两个三角形全等三角对应相等,三边对应成比例的两个三角形相似角边角ASA角角边AAS边边边SSS边角边SAS斜边与直角边HL三边的比对应相等两边的比相等且它们的夹角相等''',''''',ABACABCABCABACAA在和中，如果满足且那么能否判定这两个三角形相似呢？厘米厘米，厘米，厘米，使与画出3,5026504,EFEDEBCBABDEFABC相似吗？与DEFABC值相等吗？的与的长度，并计算出量出EFBCDEABDFACDFAC,,,ABCDEFDEFDEF命题：如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似.DEDE在线段A’B’上截取A’D=AB过点D作DEB’C’∥，交A’C’于点E.△A’DEA’B’C’∽△''''''''ADDEAEABBCAC''''ABACABAC A’D=AB已知:如图△ABC和△A`B`C`中'''''AAkCAACBAAB，求证:ABCA`B`C`△∽△又 ∠A=∠A’∴A’E=AC∴△A’DEABC(SAS)≌△∴△ABCA’B’C’∽△'''''AEACACAC∴两边对应成比例且夹角相等的两个三角形相似ABC在△ABC与△DEF中 ∠B=E∠，DEFEFBCDEAB=∴△ABCDEF∽△上述判定方法中的“角”一定只能是两对应边的夹角吗？上述判定方法中的“角”一定只能是两对应边的夹角吗？符号语言：思考？对于△ABC和△A’B’C’,如果,∠C=∠C’,这两个三角形一定相似吗?试着画画看.ABCC'B'A'DABCC'B'A'两边对应成比例且其中一边的对角对应相等的两个三角形不一定相似.相似，并说明理由是否与、根据下列条件，判断例CBAABC1cmCAcmCBcmBAcmACcmBCcmAB21,18,128,6,42）（cmCAcmBAAcmACcmABA6,3',12014,7,1201）（7''3ABAB 147''63ACAC7''''3ABACABAC两边对应成比例且夹角相等.'AA7''''3ABACABAC因为对应边的比不相等.41''123ABAB 61''183BCBC8''21ACAC'''''''''ABBCACABBCACABCABC与不相似要使两三角形相似，不改变AC的长，A’C’的长应该改为多少？5.1＝3654＝FEAE5.1＝3...