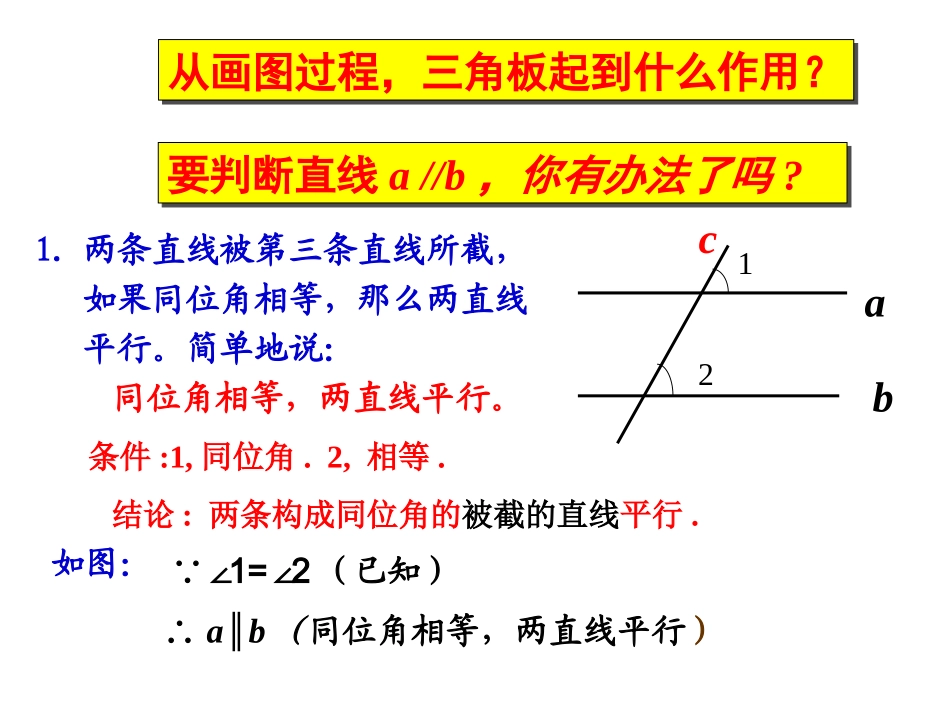
5.2平行线及其判定(第2课时)5.2平行线及其判定(第2课时)人教版七年级下册人教版七年级下册一、知识回顾一、知识回顾1、在同一平面内,两直线的位置关系有哪几种?2、怎样画两条平行的直线?从画图过程,三角板起到什么作用?从画图过程,三角板起到什么作用?要判断直线a//b,你有办法了吗?要判断直线a//b,你有办法了吗?cab121.两条直线被第三条直线所截,如果同位角相等,那么两直线平行。简单地说:同位角相等,两直线平行。∵∠1=2∠(已知)∴ab∥(同位角相等,两直线平行)如图:条件:1,同位角.2,相等.结论:两条构成同位角的被截的直线平行.大家来探索!大家来探索!①如图:如果∠1=2∠,那么a与b平行吗?abl123内错角相等,两直线平行。∵____=____(已知)∴___∥___(内错角相等,两直线平行)∠1∠2ab条件:1.内错角.2.相等.结论:两条构成内错角的被截的直线平行.②如图:如果∠1+2=180∠o,那么a与b平行吗?同旁内角互补,两直线平行。∵____+____=180o(已知)∴___∥___(同旁内角互补,两直线平行)∠1∠2ab大家来探索!大家来探索!abl12条件:1,同旁内角.2,互补.结论:两条构成同旁内角的被截的直线平行.同位角相等,两直线平行。同旁内角互补,两直线平行。内错角相等,两直线平行。直线平行的直线平行的条件例1例1①∵∠2=___(已知)∴___∥___()②∵∠3=5∠(已知)∴___∥___()③∵∠4+___=180o(已知)∴___∥___()∠6ABCDABCD∠5ABCDAC14235867BD同位角相等,两直线平行内错角相等,两直线平行同旁内角互补,两直线平行平行线的判定平行线的判定例2例2①∵∠1=_____(已知)∴ABCE∥()②∵∠1+_____=180o(已知)∴CDBF∥()③∵∠1+5=180∠o(已知)∴_____∥_____()ABCE∠2④∵∠4+_____=180o(已知)∴CEAB∥()平行线的判定平行线的判定∠3∠313542CFEADB内错角相等,两直线平行同旁内角互补,两直线平行同旁内角互补,两直线平行同旁内角互补,两直线平行例3例3如图,已知∠1=75o,2=105∠o问:AB与CD平行吗?为什么?平行线的判定平行线的判定AC1423BD53.两条直线垂直于同一条直线,这两条直线平行吗?为什么?答:垂直于同一条直线的两条直线平行.abc12练一练因为b⊥a所以∠2=90°(垂直的定义)从而b∥c.(同位角相等,两直线平行)所以∠1=90°(垂直的定义)因为c⊥a所以∠1=∠2(等量代换)解法1:理由:如图,∵b⊥a,c⊥a(已知)∴∠1=2=90°(∠垂直定义)∴b∥c(内错角相等,两直线平行)abc12解法2:理由:如图,∵b⊥a,c⊥a(已知)∴∠1=2=90°(∠垂直定义)∴∠1+2=180°∠∴b∥c(同旁内角互补,两直线平行)abc12解法3:结论在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行。bc12a已知∠3=45°,∠1与∠2互余,试说明?解:由于∠1与∠2是对顶角,∴∠1=2∠又∵∠1+2=90°(∠已知)∴∠1=2=45°∠∵∠3=45°(已知)∴∠2=3∠∴ABCD∥(内错角相等,两直线平行)123ABCDAB//CD同位角相等内错角相等同旁内角互补两直线平行平行线的判定示意图平行线的判定示意图判定数量关系位置关系