三角函数的图象与性质VIP免费

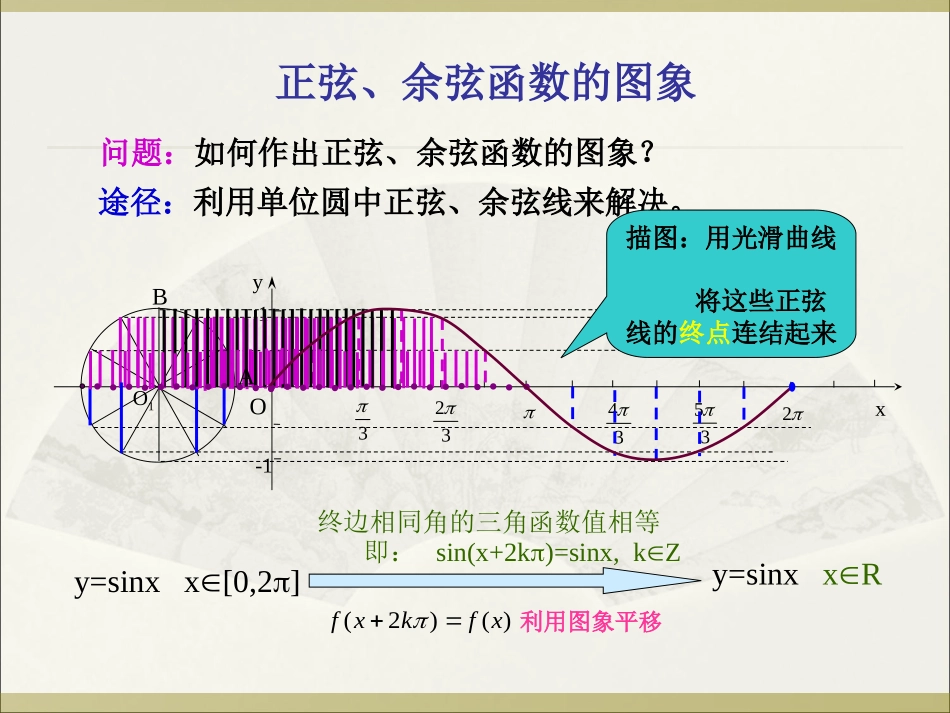
正弦、余弦函数的图象三角函数三角函数线正弦函数余弦函数正切函数正切线AT1.4.1正弦、余弦函数的图象yxO-1PMA(1,0)Tsin=MPcos=OMtan=AT正弦线MP余弦线OM复习回顾正弦、余弦函数的图象问题：如何作出正弦、余弦函数的图象？途径：利用单位圆中正弦、余弦线来解决。y=sinxx[0,2]O1Oyx33234352-11y=sinxxR终边相同角的三角函数值相等即：sin(x+2k)=sinx,kZ)()2(xfkxf描图：用光滑曲线将这些正弦线的终点连结起来利用图象平移AB正弦、余弦函数的图象x6yo--12345-2-3-41y=sinxx[0,2]y=sinxxR正弦曲线yxo1-122322x6yo--12345-2-3-41正弦、余弦函数的图象余弦函数的图象正弦函数的图象x6yo--12345-2-3-41y=cosx=sin(x+),xR2余弦曲线(0,1)(,0)2(,-1)(,0)23(2,1)正弦曲线形状完全一样只是位置不同如何由正弦函数图像得到余弦函数图像？正弦、余弦函数的图象yxo1-122322(0,0)(,1)2(,0)(,-1)23(2,0)五点画图法五点法——(0,0)(,1)2(,0)(,1)23(2,0)(0,0)(,1)2(,0)(,1)23(2,0)(0,0)(,1)2(,0)(,1)23(2,0)(0,0)(,1)2(,0)(,1)23(2,0)(0,0)(,1)2(,0)(,-1)23(2,0)(0,0)(,1)2(,0)(,-1)23(2,0)(0,0)(,1)2(,0)(,-1)23(2,0)(0,0)(,1)2(,0)(,-1)23(2,0)正弦、余弦函数的图象例1（1）画出函数y=1+sinx，x[0,2]的简图：xsinx1+sinx22302010-1012101o1yx22322-12y=sinx，x[0,2]y=1+sinx，x[0,2]步骤：1.列表2.描点3.连线正弦、余弦函数的图象（2）画出函数y=-cosx，x[0,2]的简图：xcosx-cosx2230210-101-1010-1yxo1-122322y=-cosx，x[0,2]y=cosx，x[0,2]例3.利用正弦函数和余弦函数的图象，求满足下列条件的x的集合：21sin)1(x)25,0(21cos)2(xx，例2.用五点法作函数2cos(),3yx的简图.作业：P46A组：1;B组：1选做：用“五点法”作函数：3sin(2)13yx的简图作下列函数的简图⑴y=|sinx|，⑵y=sin|x|1.4.21.4.2正、余弦函数的性质正、余弦函数的性质(2,0)(,-1)23(,0)(,1)2要点回顾.正弦曲线、余弦函数的图象1)图象作法---几何法五点法2)正弦曲线、余弦曲线x6yo--12345-2-3-41余弦曲线(0,1)(,0)2(,-1)(,0)23(2,1)x6yo--12345-2-3-41正弦曲线(0,0)新课讲解.正弦函数、余弦函数的性质(一)关于定义域例1.求下列函数的定义域：1)lgsin2)2cos3yxyx新课讲解.正弦函数、余弦函数的性质注意：如果在周期函数f(x)的所有周期中存在一个最小的正数，那么这个最小正数就叫做f(x)的最小正周期.1.周期性的定义对于函数f(x),如果存在一个非零常数T,使得当x取定义域内的每一个值时，都有f(x+T)=f(x)那么函数f(x)就叫做周期函数.非零常数T叫做这个函数的周期.(二)关于周期性新课讲解.正弦函数、余弦函数的性质2.求函数的周期例2.求下列函数的周期：1)3cos2)sin213)2sin(),26yxyxyxxR---定义法新课讲解.正弦函数、余弦函数的性质例3.求下列函数的周期：1)sin()32)cos313)3sin(),35yxyxyxxR一般结论：sin()cos(),2(,,,0,0)yAxyAxxRAAT函数及为常数的周期---利用结论P36.ex.1.2新课讲解.正弦函数、余弦函数的性质结论：正弦函数是奇函数，余弦函数是偶函数(三)关于奇偶性（复习）一般地,•如果对于函数f(x)的定义域内任意一个x,都有f(-x)=f(x)，那么就说f(x)是偶函数•如果对于函数f(x)的定义域内任意一个x,都有f(-x)=-f(x)，那么就说f(x)是奇函数新课讲解.例4.下列函数是奇函数的为：D例5.试判断函数在下列区间上的奇偶性1sincos()1sincosxxfxxx(1)(.).......(2)[.]2222xx注意大前提：定义域关于原点对称2(0811()()0,13(),()?2yfxxRfxxf四川理延考）设函数的图像关于x=0及x=1对称，且x时则14答案：(09111()(+1)(1)()()()(2)(3)fxRfxfxfxfxfx...