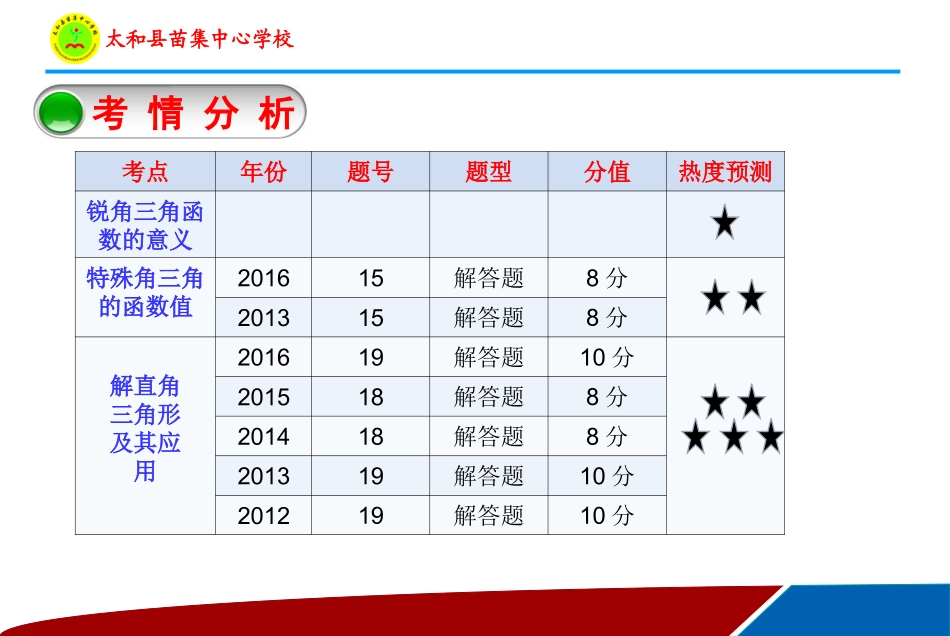
太和县苗集中心学校苗集中心学校刘振华太和县苗集中心学校1、了解解直角三角形的概念及条件;视角、方位角、坡角、坡度的概念2、理解锐角三角函数定义及特殊角的三角函数值3、掌握解直角三角形常用的关系(角的关系、三边关系、边角关系)4、运用直角三角形的常用关系解决和高度、宽度等有关的实际问题复习目标太和县苗集中心学校考情分析考情分析考点年份题号题型分值热度预测锐角三角函数的意义特殊角三角的函数值201615解答题8分201315解答题8分解直角三角形及其应用201619解答题10分201518解答题8分201418解答题8分201319解答题10分201219解答题10分太和县苗集中心学校1、解直角三角形的定义:由直角三角形中的已知元素求出其余()的过程叫解直角三角形。解直角三角形除直角外,至少知道三边两锐角中的()个元素,其中至少知道()。2、锐角三角函数定义:如图,在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,则sinA=(),cosA=(),tanA=().未知元素两个元素一个元素是边知识清单acbcab太和县苗集中心学校3、特殊角的锐角三角函数值:锐角α锐角三角函数30°45°60°sinαcosαtanα1232332222132123太和县苗集中心学校4、解直角三角形常用的关系:如图,在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,则有下列关系:(1)三边的关系:a2+b2=________;(2)角的关系:∠A+∠B=_______;(3)边与角的关系:sinA=cosB=_____,sinB=cosA=________,tanA=_____;(4)面积关系:S△ABC=________;(5)直角三角形斜边上的中线等于斜边的_______。(6)若斜边上的高为h,则满足a、b、c、h的关系式是_______。c2∠cacbcabab21一半ab=ch太和县苗集中心学校5.解直角三角形的实际问题(1)仰角:在视线与水平线所成的角中,视线在水平线的角叫做仰角(2)俯角:在视线与水平线所成的角中,视线在水平线的角叫做俯角(3)坡度:坡面的铅直高度h和水平宽度l的比叫做坡面的坡度(或坡比),记作i=________(4)坡角:坡面与水平面的夹角叫做坡角,记作α,i=,坡度越大,α角越大,坡面________(5)指北或指南方向线与目标方向线所成的小于90°的角叫做方向角上方下方h∶l越陡tanα太和县苗集中心学校考题热身1.【2016·安徽】如图19-1,河的两岸l1与l2相互平行,A,B是l1上的两点,C,D是l2上的两点,某人在点A处测得∠CAB=90°,∠DAB=30°,再沿AB方向前进20米到达点E(点E在线段AB上),测得∠DEB=60°,求C,D两点间的距离.图19-1太和县苗集中心学校解:过点D作l1的垂线,垂足为F, ∠DEB=60°,∠DAB=30°,∴∠ADE=∠DEB-∠DAB=30°,∴△ADE为等腰三角形,∴DE=AE=20.在Rt△DEF中,EF=DE·cos60°=20×12=10. DF⊥AF,∴∠DFB=90°,∴AC∥DF.又已知l1∥l2,∴CD∥AF,∴四边形ACDF为矩形,∴CD=AF=AE+EF=30.故C,D两点间的距离为30米.F图19-1太和县苗集中心学校2.【2015·安徽】如图19-2,平台AB高为12米,在B处测得楼房CD顶部点D的仰角为45°,底部点C的俯角为30°,求楼房CD的高度.(≈1.7)图19-23E解:如图,过点B作BE⊥CD于点E,根据题意,∠DBE=45°,∠CBE=30°. AB⊥AC,CD⊥AC,∴四边形ABEC为矩形,∴CE=AB=12.在Rt△CBE中,BE==,在Rt△BDE中,由∠DBE=45°,得DE=BE=.∴CD=CE+DE=12×(+1)≈32.4(米).故楼房CD的高度约为32.4米.30tanCE3123123太和县苗集中心学校3.[2014·安徽]如图19-3,在同一平面内,两平行高速公路l1和l2间有一条“z”型道路连通,其中AB段与高速公路l1成30°角,长为20km,BC段与AB,CD段都垂直,长为10km,CD段长为30km,求两高速公路间的距离.(结果保留根号)图19-3太和县苗集中心学校解:如图,过点A作AB的垂线交DC的延长线于点E,过点E作l1的垂线与l1,l2分别交于点H,F,则HF⊥l2.由题意知AB⊥BC,BC⊥CD,又AE⊥AB,∴四边形ABCE为矩形,∴AE=BC,AB=EC,∴DE=DC+CE=DC+AB=50.又 AB与l1成30°的角,∴∠EDF=30°,∠EAH=60°.在Rt△DEF中,EF=DE·sin30°=50×=25.在Rt△AEH中,EH=AE·sin60°=10×=∴HF=EF+HE=25+即两条高速公路间的...