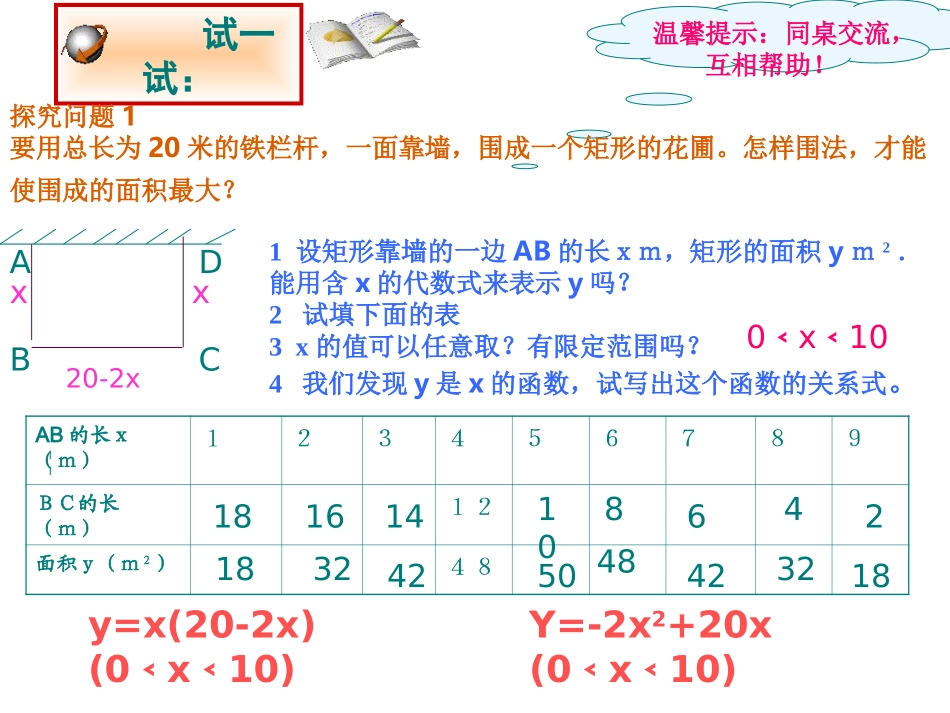
二次函数的概念知识回顾1.一元二次方程的一般形式是什么?2。一次函数的定义是什么?ax2+bx+c=0形如y=kx+b(其中k,b为常数且k≠0)的函数叫做x的一次函数(a≠0)温馨提示:同桌交流,互相帮助!试一试:探究问题1要用总长为20米的铁栏杆,一面靠墙,围成一个矩形的花圃。怎样围法,才能使围成的面积最大?1设矩形靠墙的一边AB的长xm,矩形的面积ym2.能用含x的代数式来表示y吗?2试填下面的表3x的值可以任意取?有限定范围吗?4我们发现y是x的函数,试写出这个函数的关系式。BCDAB的长x(m)123456789BC的长(m)12面积y(m2)48Axx20-2xy=x(20-2x)(0x10)﹤﹤Y=-2x2+20x(0x10)﹤﹤1818321442161050848642432180x10﹤﹤2探究问题2某商店将每商品进价为8元的商品按每10元出售,一天可售出约100件。该店想通过降低售价、增加销售量的办法来提高利润。经市场调查,发现这种商品单价每降低0.1元,其销售量可增加约10件。将这种商品的售价降低多少时,能使销售利润最大?1设每件商品降低x元(0≤x≤2),该商品每天的利润为y,y是x的函数吗?为什么要限定x的值?2怎样写出该关系式?试一试:温馨提示:同桌交流,互相帮助!单件利润(元)每天销量(件)每天利润(y元)降价x元前降价x元后100(10-8)×10010-810-x-8(10-x-8)(100+100x)100+100xy=(10-x-8)(100+100x)即y=-100x2+100x+200(0≤x≤2)每天利润=单件利润×每天销量讨论得到的两个函数关系式有什么特点?温馨提示:同桌交流,互相帮助!答(1)右边都是关于x的整式.(2)自变量x的最高次数是2.即都是自变量的二次整式!观察(1)Y=-2x2+20x(0﹤x﹤10)(2)y=-100x2+100x+200(0≤x≤2)提问对比一次函数归纳二次函数的定义?概念引入二次函数的定义:形如y=ax2+bx+c(a,b,c是常数,a≠0)的函数叫做x的二次函数驶向胜利的彼岸提问:1.上述概念中的a为什么不能是0?2.对于二次函数y=ax2+bx+c中的b和c可否为0?若b和c各自为0或均为0,上述函数的式子可以改写成怎样?你认为它们还是不是二次函数?二次函数的特殊形式:当b=0时,y=ax2+c当c=0时,y=ax2+bx当b=0,c=0时,y=ax2注意:(1)必须a≠0,否则就不是二次函数,而b、c两数可以是0(2)在y=ax2+bx+c(a≠0)中,x的取值范围是全体实数但当自变量表示实际意义时,自变量的取值范围就不一定是全体实数思考:二次函数的一般式y=ax2+bx+c(a≠0)与一元二次方程ax2+bx+c=0(a≠0)有什么联系和区别?驶向胜利的彼岸联系:(1)等式一边都是ax2+bx+c且a≠0(2)方程ax2+bx+c=0可以看成是函数y=ax2+bx+c中y=0时得到的.区别:前者是函数.后者是方程.等式另一边前者是y,后者是0知识运用例1:下列函数中,哪些是二次函数?(1)y=3x-1()(2)y=3x2()(3)y=3x3+2x2()(4)y=2x2-2x+1()(5)y=x-2+x()(6)y=x2-x(1+x)()不是是不是不是是不是驶向胜利的彼岸例2.当m取何值时,函数是y=(m+2)x分别是1.一次函数?m2-22.二次函数?知识运用达标测试1.下列函数中,哪些是二次函数?(1)y=3(x-1)+1²(3)s=3-2t²(5)y=(x+3)-x²²(6)v=10πr²21(4)y=x-x(是)(否)(是)(否)(否)(是)(7)y=x+x+25²³(8)y=2+2x²(否)(否)1y=x+x(2)2007年11月13日制作原创徐继伦如果函数y=(k-3)+kx+1是二次函数,则k的值一定是______2k-3k+2x02如果函数y=+kx+1是二次函数,则k的值一定是______2k-3k+2x0,33:m取何值时,函数y=(m+1)x+(m-3)x+m是二次函数?122mm解:由题意得m2—2m-1=2m+1≠0∴m=3知识的升华已知函数(1)k为何值时,y是x的一次函数?(2)k为何值时,y是x的二次函数?解(1)根据题意得∴k=1时,y是x的一次函数。002kkk22()2ykkxkxk当时数2(2)k-k≠0,即k≠0且k≠1y是x的二次函小结拓展驶向胜利的彼岸你认为今天这节课最需要掌握的是________________。