直线与平面平行的判定VIP免费

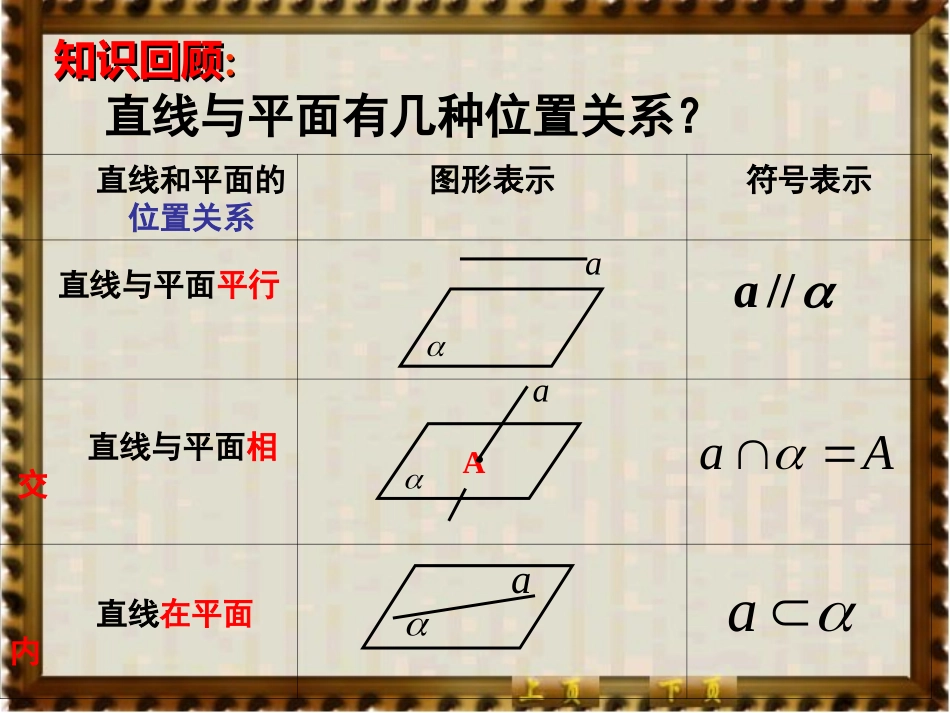
2.2.1直线与平面平行的判定直线和平面的位置关系图形表示符号表示aaA直线在平面内直线与平面相交直线与平面平行知识回顾知识回顾：：直线与平面有几种位置关系？aaAa//a复习复习直线与平面平行直线与平面平行定义定义：：一条直线和一个平面没有公共点，一条直线和一个平面没有公共点，叫做直线与平面平行叫做直线与平面平行..以上知识点都能熟练掌握吗a怎样判定直线与平面平行呢？引入新课引入新课根据定义，判定直线与平面是否平行，只需判定直线与平面有没有公共点．但是，直线无限延长，平面无限延展，如何判断直线与平面没有公共点呢？a探究在生活中，注意到门扇的两边是平行的．当门扇绕着一边转动时，另一边始终与门框所在的平面没有公共点，此时门扇转动的一边与门框所在的平面给人以平行的印象．实例感受实例感受11日常生活处处体现数学从实际问题认识数学用数学来研究实际问题门扇转动的一边AB与门框所在的平面（墙面）之间的位置关系．BA1A1BABAB将一本书平放在桌面上，翻动书的硬皮封面，封面边缘AB所在直线与桌面所在平面具有什么样的位置关系？实例感受实例感受22探究问题，归纳结论如图，平面外的直线平行于平面内的直线b。（1）这两条直线共面吗？（2）直线与平面相交吗？baaa直线在平面外有两种：直线与平面相交，直线与平面平行aAa直线在平面外直线与平面平行的判定定理：平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行.简述为：线线平行线面平行ababa//a//b图形语言符号语言①外②内③平行线面平行线线平行转化转化思想：感受校园生活中线面平行的例子:天花板平面定理的应用例1.如图，空间四边形ABCD中，E、F分别是AB，AD的中点.求证：EF∥平面BCD.ABCDEF分析：要证明线面平行只需证明线线平行，即在平面BCD内找一条直线平行于EF，由已知的条件怎样找这条直线？空间四边形的画法参考上图证明：连结BD.在△ABC中∵E、F分别是AB，AD的中点∴EF∥BD（三角形中位线性质）例1.如图，空间四边形ABCD中，E、F分别是AB，AD的中点.求证：EF∥平面BCD.ABDEF定理的应用EF//BCD平面EFBCDBDBCD又平面平面Ｃ注意1：证明直线与平面平行线面平行线线平行注意2：能够运用定理的条件是要满足三条：“外、内、平行”。注意3:运用定理的关键是找平行线。找平行线又经常会用到三角形中位线定理。aba//a//b数学思想方法：转化的思想转化1.如图，在空间四边形ABCD中，E、F分别为AB、AD上的点，若，则EF与平面BCD的位置关系是_____________.AEAFEBFDEF//平面BCD变式1:ABCDEF变式2:ABCDFOE2.如图,四棱锥A—DBCE中,O为底面正方形DBCE对角线的交点,F为AE的中点.求证:AB//平面DCF.(04年天津高考)分析:连结OF,可知OF为△ABE的中位线,所以得到AB//OF.1．如图，长方体中，DCBAABCDAABCCDD（1）与AB平行的平面是；（2）与平行的平面是；（3）与AD平行的平面是；AA平面DCBADDCC平面DDCC平面平面CBCB平面DCBA平面CBCB随堂练习随堂练习B分析：要证BD1//平面AEC即要在平面AEC内找一条直线与BD1平行.根据已知条件应该怎样考虑辅助线?巩固练习:2.如图,正方体ABCD-A1B1C1D1中，E为DD1的中点，求证:BD1//平面AEC.ED1C1B1A1DCBAO证明:连结BD交AC于O,连结EO.∵O为矩形ABCD对角线的交点,∴DO=OB,又∵DE=ED1,∴BD1//EO.1//BDAEC平面ED1C1B1A1DCBAO巩固练习:如图,正方体ABCD-A1B1C1D1中，E为DD1的中点，求证:BD1//平面AEC.1BDAECEOAEC又平面平面2.注意六个字:（1）面外，（2）面内，（3）平行。小结：1.直线与平面平行的判定：(1)运用定义；(2)运用判定定理：线线平行线面平行3.关键是找平行线方法一：三角形的中位线定理；方法二：平行四边形的平行关系。