圆拄的侧面展开图VIP专享VIP免费

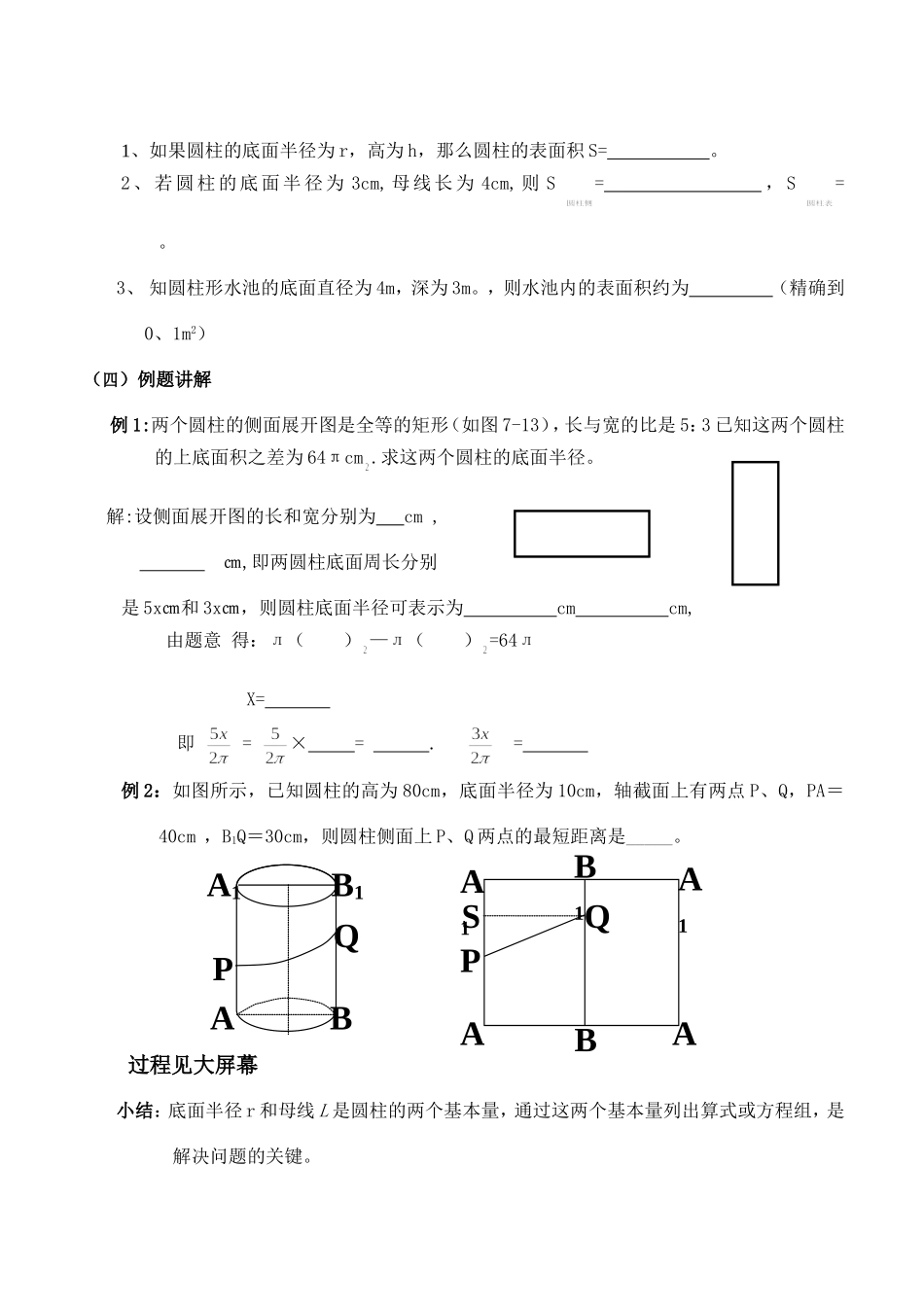
2006年江苏省数学初三数学教、学案（圆柱的侧面展开图）-苏教版[原创]授课人：袁堂彩地点：多媒体教室一、教学目标：（见大屏幕）1、解圆柱的构成及其侧面展开图的形状2、能利用矩形与圆的面积公式计算圆柱的表面积3、情感目的：感受数学来源于生活又应用于生活，培养学生观察图形、分析图形和初步的三维空间观念。二、教学重点：1、圆柱的构成与侧面展开图2、圆柱侧面展开图与r、L的关系3、圆柱侧面积及表面积的有关计算三、教学难点“转化”（把现实问题转化成数学问题即r、L的判断）四、教法：以学生观察、练习为主、教师点拔为辅，学生自主归纳总结。五、教学过程（一）课前预习；1、若圆的半径为r、则C=，S=。2、点动成、线动成、面动成。（二）新课导入：1、观看大屏幕：由庄严、雄伟、壮观的帕特农神庙带领学生进入圆柱世界。帕特农神庙呈长方形,由白色大理石筑成,周围有46根圆柱形大石柱,立在三层基座上。神庙用于奉祀雅典娜女神。2、举几个现实生活中和圆柱有关的实例，这节课我们就来研究圆柱的有关问题。（三）新课讲解一、圆柱的侧面展开图1．基本概念：圆柱的轴，圆柱的侧面，圆柱的底面，圆柱的高，母线2．基本特征：（1）圆柱的轴通过上，下底面的圆心，并且垂直底面；（2）圆柱的母线长都相等，并且都等于圆柱的高；（3）圆柱两底面平行，并且是半径相等的两个等圆，因此面积相等；（4）经过圆柱轴的平面截得的截面是矩形3．圆柱的侧面展开图：教法：这一过程由教师通过几何画板动画演示出来，让学生自己去发现规律。1、圆柱的侧面展开图是一个矩形。这个矩形的一边长等于，另一边长等于。2、如果圆柱底面半径为r、侧面母线长为L，那么它的侧面积=，它的表面积S表=。3、圆柱的轴截面是一个形，这个矩形的一边长等于，另一边长等于结论：=2лrlS=2лrl+2лr基础训练：AC1D1BDC2D2C1、如果圆柱的底面半径为r，高为h，那么圆柱的表面积S=。2、若圆柱的底面半径为3cm,母线长为4cm,则S=，S=。3、知圆柱形水池的底面直径为4m，深为3m。，则水池内的表面积约为（精确到0、1m2）（四）例题讲解例1:两个圆柱的侧面展开图是全等的矩形（如图7-13），长与宽的比是5：3已知这两个圆柱的上底面积之差为64πcm.求这两个圆柱的底面半径。解:设侧面展开图的长和宽分别为cm,㎝,即两圆柱底面周长分别是5x㎝和3x㎝，则圆柱底面半径可表示为cmcm,由题意得：л（）—л（）=64лX=即=×=.=例2：如图所示，已知圆柱的高为80cm，底面半径为10cm，轴截面上有两点P、Q，PA＝40cm，B1Q＝30cm，则圆柱侧面上P、Q两点的最短距离是_____。过程见大屏幕小结：底面半径r和母线L是圆柱的两个基本量，通过这两个基本量列出算式或方程组，是解决问题的关键。A1B1PQABAABQSPA1B1A1（五）课堂检测1、如果圆柱的两底面积之和等于侧面积，那么母线与底面直径之比等于。2、用两张全等的矩形纸分别卷成两个形状不同的柱面（即圆柱的侧面）。设较高圆柱的侧面积和底面半径分别为S1和r1，较矮圆柱的侧面积和底面半径分别为S2和R2,那么()(A)S1=S2,r1=R2(B)S1=S2,r1＞R2(C)S1=S2,r1＜R2(D)S1≠S2,r1=R21、3、一矩形纸板,两边长分别为2cm和4cm,绕一边所在直线旋转一周所形成几何体的表面积为()(A)24πcm2(B)24πcm2或48πcm2(C)20πcm2(D)20πcm2或48πcm24.有一块长度足够而宽度为32cm的矩形铁皮,要做一个底面直径和高都是32cm的圆柱形无盖水桶,不计剪接时所耗用的材料,需裁下多长的铁皮?(精确到0.1cm)5、（2004贵州贵阳）我国古代数学中有这样一道数学题：有一棵树直立在地上，树高2丈，粗3尺，有一根藤条从树根缠绕而上，缠绕7周到达树顶，请问这根藤有多长？（注：枯树可以看成圆柱；树粗3尺，指的是：圆柱截面周长为3尺。1丈＝10尺）