同角三角函数的基本关系VIP免费

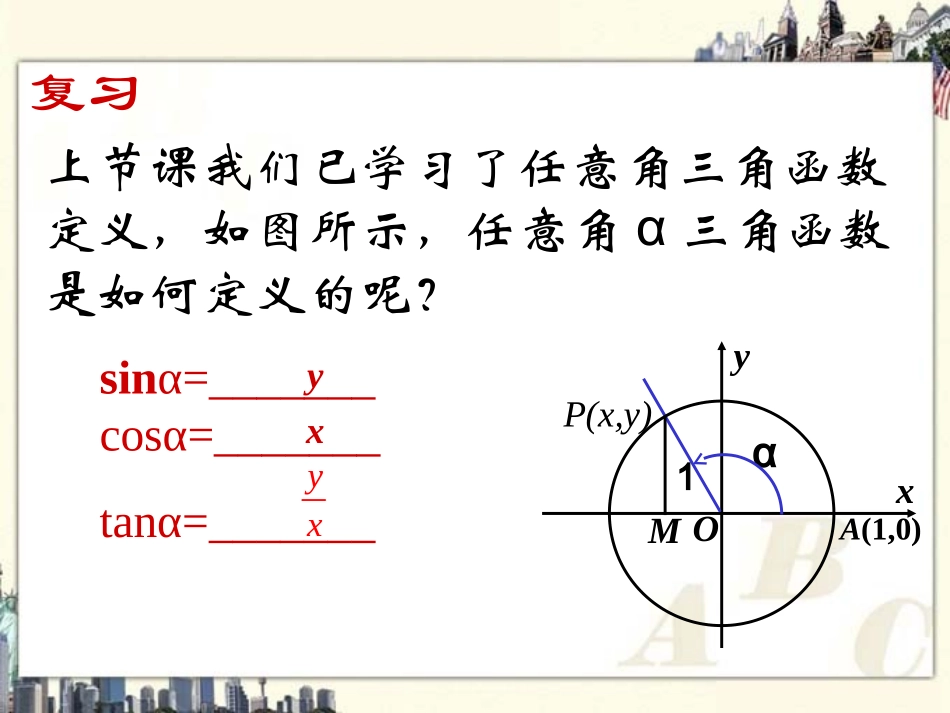
同角三角函数的基本关系上节课我们已学习了任意角三角函数定义，如图所示，任意角α三角函数是如何定义的呢？复习P(x,y)Oxy1MA(1,0)αsinα=_______cosα=_______tanα=_______yxyxOxy1MA(1,0)α在RtOMP△中,由勾股定理有MP2+OM2=P(x,y)y2+x2=1sin2α+cos2α=1根据三函数的定义当2kkZsintancos同一个角α的正弦、余弦的平方和等于1，商等于角α的正切.OP2=11cossin22cossintan①平方关系：②商数关系：同角三角函数的基本关系式总结如下：36sin,cos,tan.5例已知求的值解:因为sinα<0,sinα≠1,所以α是第三或第四象限角22sincos1由得22cos1sin23161525如果α是第三象限角,那么cosα<0.于是164cos255如果α是第四象限角,那么4cos53tan443)45()53(cossintan堂上练习41.cos,..5已知且是第三象限角求sin,tan的值2.tan3,sin,cos.已知求的值22sin3cos:sincos1解33sinsin2211coscos22或229sin1cos25因α是第三角限角所以3sin5sin3tancos4cos1sin=1sin1sinxxxx左证法1:由cosx≠0,知sinx≠-1,所以1+sinx≠0,于是2cos1sin=1sinxxx2cos1sin=cosxxx1sin=cosxx右xxxxcossin1sin1cos7、求证：例证法2:因为1-sin1sinxx21sinxcoscosxx且1-sinx≠0,cosx≠0,所以cos1sin1sincosxxxx222cos11costan;212sin4.化简堂上练习sin1costancossincos222222222cossincos2cos1212sinsincos2sin2222cossin1cossin5.求证:堂上练习22221sincossincos左22sincos=右22222=sinsincoscos左22=sincos1右.1coscossinsin)2(;cossincossin)1(22242244（1）同角三角函数的关系式的前提是“同角”，（2）条件等式，即它们成立的前提是表达式有意义．cossintan（3）利用平方关系时，往往要开方，因此要先根据角所在象限确定符号，即要就角所在象限进行分类讨论.小结1cossin22cossintan①平方关系：②商数关系：作业课本第24页习题1.2A组10,11,13