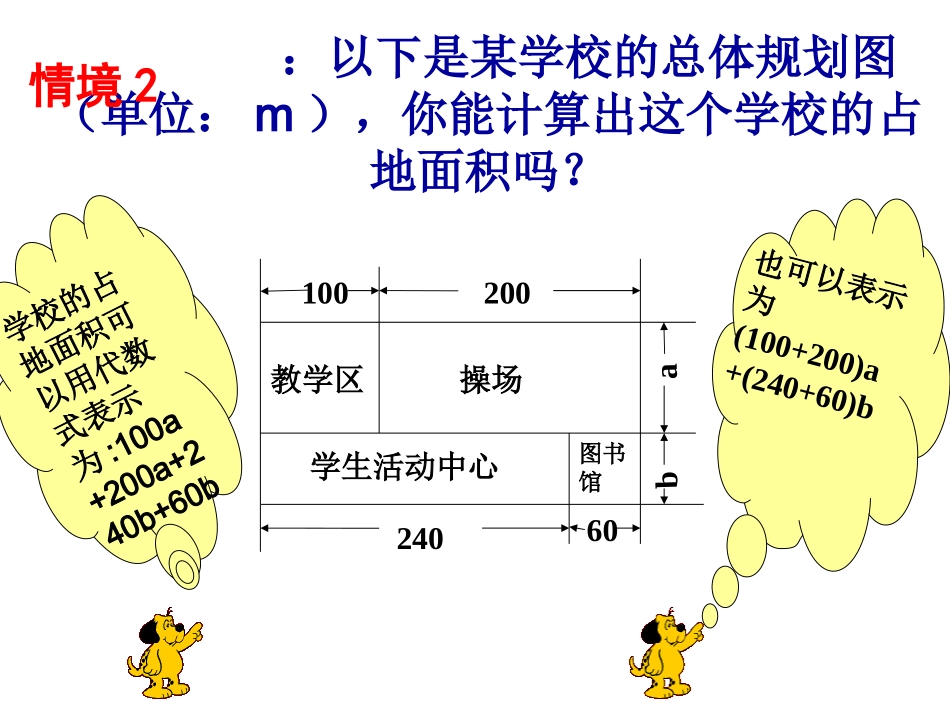
七年级数学备课组2014.10课题:星期天,小明上街买了4个苹果,8个橘子,7个香蕉。妈妈不知道小明已经买了水果,于是,下班后妈妈从街上又买来5个苹果,10个橘子,6个香蕉,问:苹果,橘子,香蕉一共各有多少个?你是怎么求和的?:以下是某学校的总体规划图(单位:m),你能计算出这个学校的占地面积吗?也可以表示为(100+200)a+(240+60)b100200教学区操场学生活动中心图书馆24060ab学校的占地面积可以用代数式表示为:100a+200a+240b+60b情境2100a与200a;240b与60b;5ab2与-13ab2;-9x2y3与5x2y3有什么共同的特点?所含字母相同,并且相同字母的指数相同2abac与3;abba与-22abcabc与abmabn与0.59与(1)(3)(5)(2)(4)(6)22218xyxy与判断下列各组单项式是否同类项?所含字母相同,并且相同字母的指数也相同的项,叫做同类项.(两个单独的数也叫同类项)×××√√√如何判断同类项:1、两同:一是所含字母相同,二是相同字母的指数也相同,两者缺一不可2、同类项与系数的大小无关3、同类项与它们所含字母的顺序无关4、所有的常数项都是同类项思维拓展:(1)请你说出一个9xy2的同类项((22)已知)已知2x2x22yynn与与––3x3xmmyy44是同是同类项,类项,则则m=m=,,n=n=。423+2=()553+2=()aaa+=(1)7a-3a(2)4x2+2x2(3)5ab2-13ab2(4)–9x2y3+5x2y3=(7-3)a=4a===合并同类项的法则:6x2-8ab2-4x2y3(4+2)x2=(5-13)ab2=(-9+5)x2y3=合并同类项,并说明你计算的理由:根据乘法对加法的分配律把同类项合并成一项,叫做合并同类项。把同类项的系数相加,所得的结果做为系数,字母和字母的指数不变。合并同类项的法则同类项的系数相加,所得的结果作为系数,字母和字母的指数不变。例合并同类项(1)-3x+2y-5x-7y解:原式=(-3x-5x)+(2y-7y)加法交换律、结合律=(-3-5)x+(2-7)y乘法对加法的分配律=-8x-5y有理数加法法则例题例题评讲评讲例2:合并同类项-4ab+8a-2b2-9ab–8a解:-4ab+8a-2b2-9ab–8a=(-4ab-9ab)=()ab+()a=-13ab合并同类项步骤:1、划线,找出各组同类项;2、把同类项写在一起;3、合并同类项。注意:不要漏写没有同类项的项,如-2b2。+(+8a–8a)-2b2-4-9+8–8-2b2-2b2例题例题评讲评讲找移并一、下列各题的结果是否正确?如有错误,请指出错误的地方。1、16y2-7y2=92、7x–5x=2x23、3x+3y=6xy4、19a2b-9b2a=10合并同类项时,字母不变。应为:16y2-7y2=9y2合并同类项时,字母的指数不变。应为:7x–5x=2x没有同类项可合并没有同类项可合并课堂课堂练习练习通过以上的练习你能找出合并同类项的要点是什么吗?一变二不变一变--------系数要变(新系数变为原来各系数的和)二不变-------字母和字母的指数不变(原来的字母和字母的指数照抄)二、填空(1)2xy+()=7xy5xy(2)m2+m+()+()-1=3m2-2m-12m2-3m三、合并同类项(1)a2-3a-3a2+a2+2a-7(2)x2-5xy+yx+2x2我们这节课学到了什么?同类项同类项合并同类项合并同类项两个相同两个相同法则法则((11)所含字母相同)所含字母相同((22)相同字母的指数)相同字母的指数也相同;也相同;((11)系数相加作为)系数相加作为结果的系数。结果的系数。((22)字母与字母的)字母与字母的指数不变。指数不变。把(a+b)看做一个字母,合并3(a+b)-(a+b)+2(a+b)-0.2(a+b)中的同类项:3(a+b)-(a+b)+2(a+b)-0.2(a+b)=(3-1+2-0.2)(a+b)=3.8(a+b)请你仿照上面的方法,合并下列各式中的同类项:5(x+y)+4(x+y)-10(x+y)《补充习题》P44