三垂线定理及逆定理(二)VIP免费

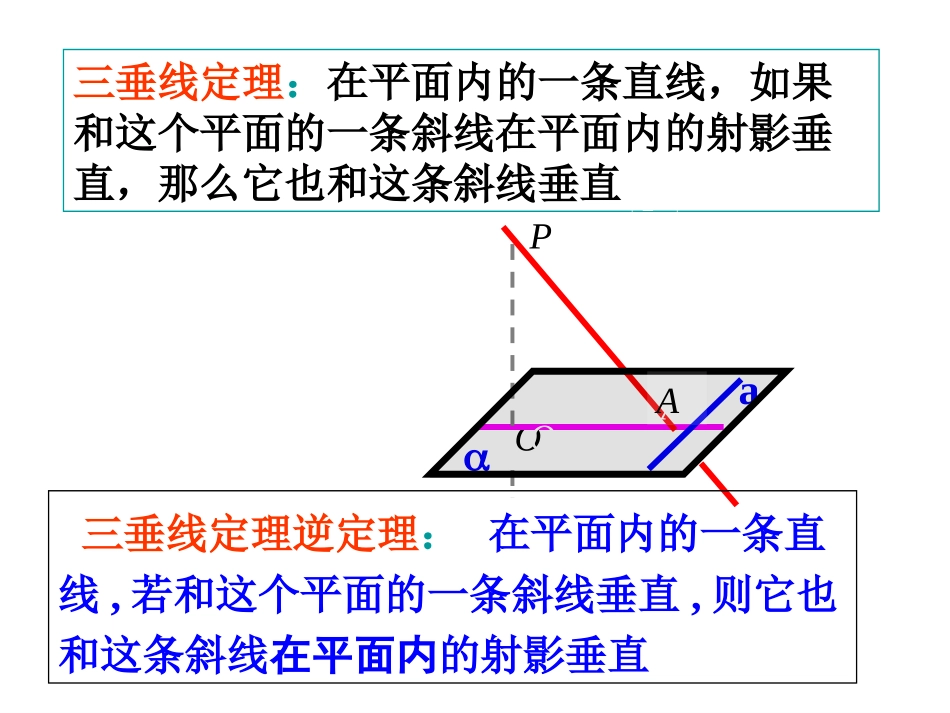
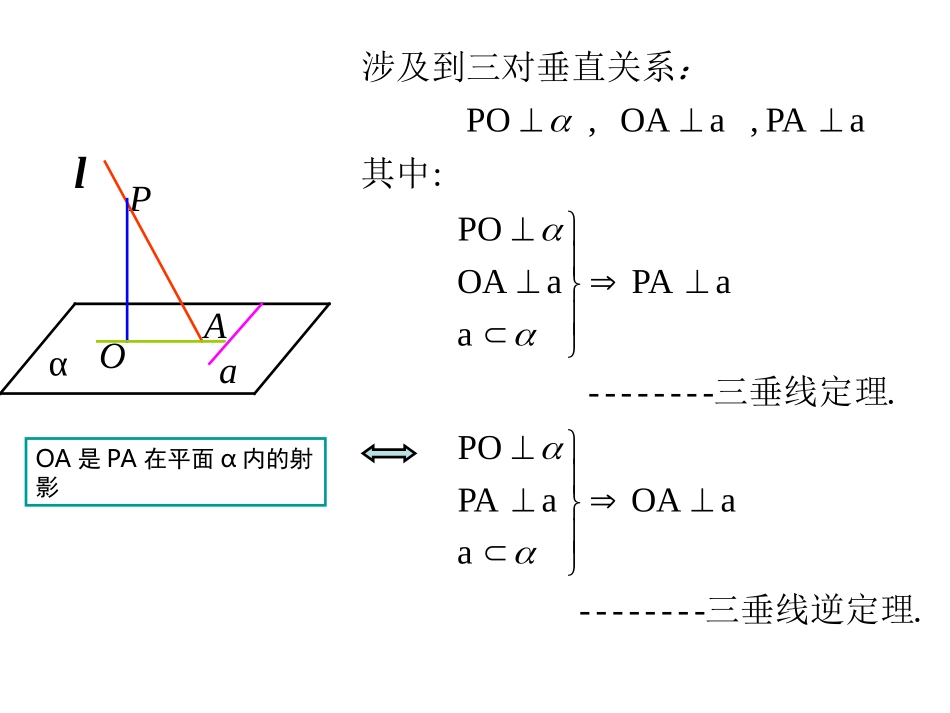
三垂线定理及其逆定理(二)OPOaAA三垂线定理：在平面内的一条直线，如果和这个平面的一条斜线在平面内的射影垂直，那么它也和这条斜线垂直三垂线定理逆定理：在平面内的一条直线,若和这个平面的一条斜线垂直,则它也和这条斜线在平面内的射影垂直PAAPOαla.--------aOAaaPAPO.--------aPAaaOAPO:aPA,aOA,PO三垂线逆定理三垂线定理其中涉及到三对垂直关系：OA是PA在平面α内的射影例1、若一个角所在平面外一点到角的两边距离相等,则这一点在平面上的射影在这个角的平分线上PABCOEFαα已知:∠BAC在平面α内,点Pα,PE⊥AB,PF⊥AC,PO⊥α,垂足分别是E,F,O,PE=PF求证:∠BAO=∠CAO•[练习]•1、如果过角顶点的一条平面斜线和角的两边的夹角相等,那么这条斜线在平面内的射影在角平分线所在的直线上.PABCOEFαα[例2]：如图，∠BOC在平面α内，OA是α的斜线，若∠AOB=AOC=60∠0,BOC=90∠0，求OA和平面α所成的角.OABCαH2.,..BACPAPAaPO0已知在平面内,是的斜线,PO于O,若PAB=PAC=BAC=60则•[练习]•例3、如图，已知PA⊥矩形ABCD所在平面，M，N分别是AB，PC的中点。•（1）求证：MNCD⊥；•（2）若∠PDA=450，求证：MN⊥平面PCD.PABCDMN