反比例函数与实际问题1VIP免费

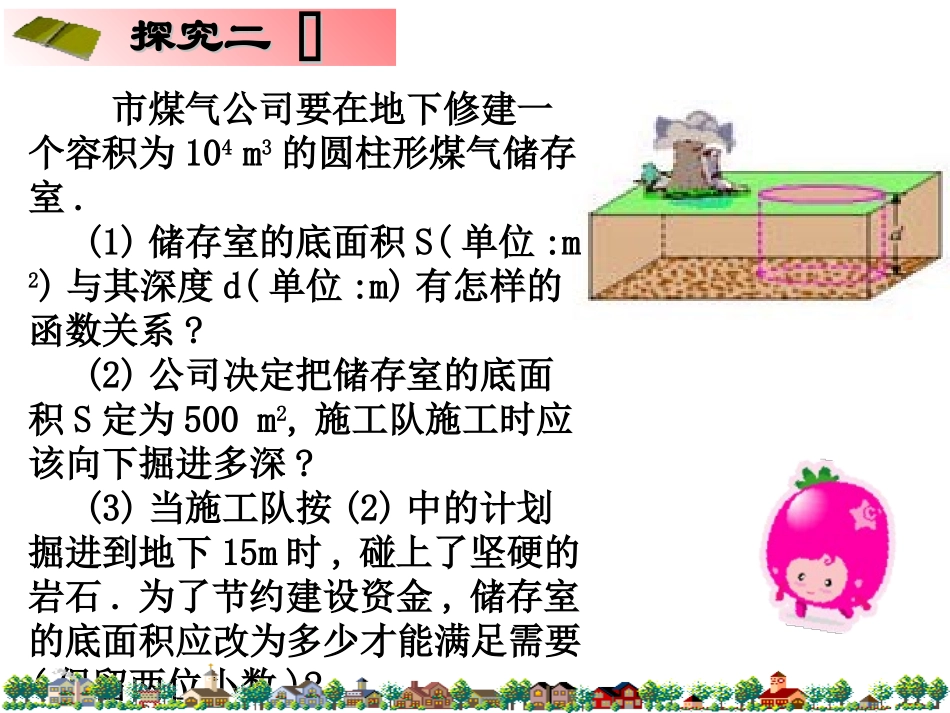
你吃过拉面吗？你知道在做拉面的过程中渗透着数学知识吗？（1）体积为20cm3的面团做成拉面，面条的总长度y与面条粗细（横截面积）s有怎样的函数关系？（2）某家面馆的师傅手艺精湛，他拉的面条粗1mm2，面条总长是多少？探究一市煤气公司要在地下修建一个容积为104m3的圆柱形煤气储存室.(1)储存室的底面积S(单位:m2)与其深度d(单位:m)有怎样的函数关系?(2)公司决定把储存室的底面积S定为500m2,施工队施工时应该向下掘进多深?(3)当施工队按(2)中的计划掘进到地下15m时,碰上了坚硬的岩石.为了节约建设资金,储存室的底面积应改为多少才能满足需要(保留两位小数)?探究二探究二解解::(1)(1)根据圆柱体的体积公式根据圆柱体的体积公式,,我们有我们有s×d=s×d=104变形得变形得即储存室的底面积即储存室的底面积SS是其深度是其深度dd的反比例函数的反比例函数..dS104市煤气公司要在地下修建一个容积为104m3的圆柱形煤气储存室.(1)储存室的底面积S(单位:m2)与其深度d(单位:m)有怎样的函数关系?把把S=500S=500代入代入,,得得dS104d104500解得解得d=20d=20如果把储存室的底面积定为如果把储存室的底面积定为500500,,施工时应向地下掘进施工时应向地下掘进20m20m深深..m2(2)公司决定把储存室的底面积S定为500m2,施工队施工时应该向下掘进多深?解解::根据题意根据题意,,把把d=15d=15代入代入,,得得15104s解得解得S≈666.67S≈666.67当储存室的深为当储存室的深为15m15m时时,,储存室的底面积应改为储存室的底面积应改为666.67666.67才能满足需要才能满足需要..m2dS104(3)当施工队按(2)中的计划掘进到地下15m时,碰上了坚硬的岩石.为了节约建设资金,储存室的底面积应改为多少才能满足需要(保留两位小数)?解解::例题码头工人以每天30吨的速度往一艘轮船上装载货物,把轮船装载完毕恰好用了8天时间.(1)轮船到达目的地后开始卸货,卸货速度v(单位:吨/天)与卸货时间t(单位:天)之间有怎样的函数关系?(2)由于遇到紧急情况,船上的货物必须在不超过5日内卸载完毕,那么平均每天至少要卸多少吨货物?例题码头工人以每天30吨的速度往一艘轮船上装载货物,把轮船装载完毕恰好用了8天时间.(1)轮船到达目的地后开始卸货,卸货速度v(单位:吨/天)与卸货时间t(单位:天)之间有怎样的函数关系?(2)由于遇到紧急情况,船上的货物必须在不超过5日内卸载完毕,那么平均每天至少要卸多少吨货物?根据装货速度×装货时间=货物的总量，可以求出轮船装载货物的总量；再根据卸货速度=货物的总量÷卸货时间，得到v与t的函数式。解：解：（1）设轮船上的货物总量为k吨，则根据已知条件有k=30×8=240所以v与t的函数式为tv240（2）把t=5代入，得tv240485240v结果可以看出，如果全部货物恰好用5天卸完，则平均每天卸载48吨.若货物在不超过5天内卸完,则平均每天至少要卸货48吨.思考:还有其他方法吗?图象法图象法不等式法不等式法(2)由于遇到紧急情况,船上的货物必须在不超过5天内卸载完毕,那么平均每天至少要卸多少吨货物?解:由题意知t≤548524005240,5240240vvvvtvttv所以又得有解法2已知矩形的面积为24，则它的长y与宽x之间的关系用图像大致可表示为（）上题中，当矩形的长为12cm时，宽为_______，当矩形的宽为4cm，其长为________.如果要求矩形的长不小于8cm，其宽至多要________.已知一个矩形的面积为20㎡,相邻的两边长分别是xm和ym,那么:(1)写出y与x之间的函数关系(2)画出y与x之间的函数图象.(3)若矩形的一边长不小于4,求另一边长的取值范围.实际问题反比例函数建立数学模型运用数学知识解决（2）d＝30(cm)ds3000)1(如图，某玻璃器皿制造公司要制造一种容积为1升(1升＝1立方分米)的圆锥形漏斗．(1)漏斗口的面积S与漏斗的深d有怎样的函数关系?(2)如果漏斗口的面积为100厘米2，则漏斗的深为多少?随堂练习自我发展的平台随堂练习自我发展的平台1.有一面积为60的梯形，其上底长是下底长的，若下底长为x，高为y，则y与x的函数关系是________．132.小明家用购电卡买了1000度电，那么这些电能够使用的天数y与平均每天用电度数x之间的函数关系式是________，如果平均每天用5度，这些电可以用______天...