七年级数学上册一元一次方程的复习课件VIP免费

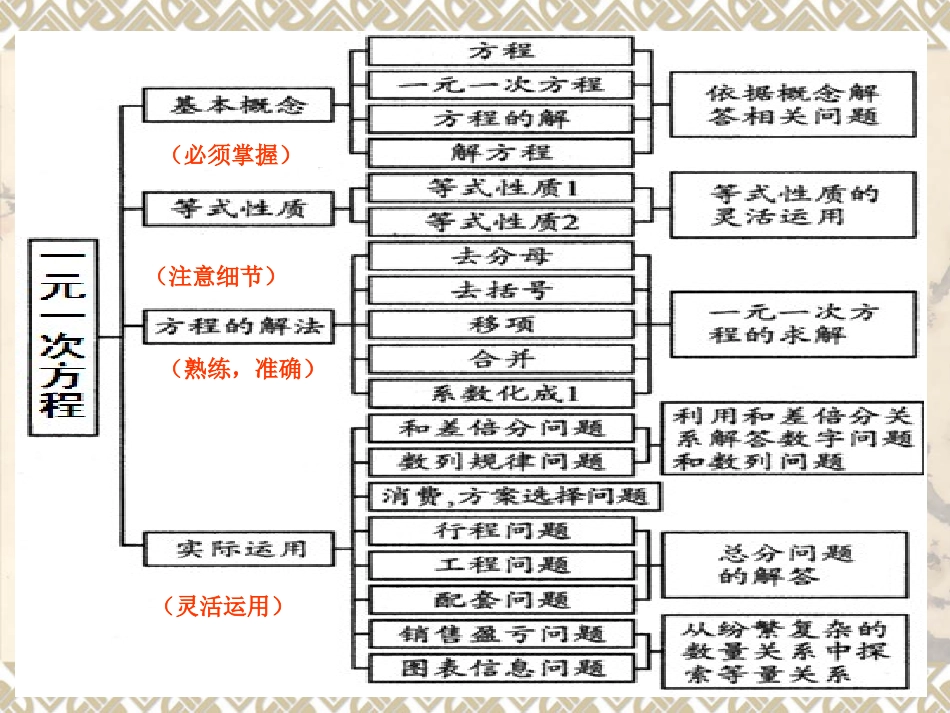
（必须掌握）（注意细节）（熟练，准确）（灵活运用）知识点：一、方程的有关概念1、方程的概念：（1）含有未知数的等式叫方程。（2）在一个方程中，只含有一个未知数，并且未知数的指数是1，系数不为0，这样的方程叫一元一次方程。二、等式的基本性质：（1）等式两边同时加上（或减去）同一个代数式，所得结果仍是等式。若a=b，则a+c=b+c或a–c=b–c。（2）等式两边同时乘以（或除以）同一个数（除数不能为0），所得结果仍是等式。解一元一次方程的步骤主要依据注意问题1、去分母等式的性质2注意拿这个最小公倍数乘遍方程的每一项，切记不可漏乘某一项，分母是小数的，要先利用分数的性质，把分母化为整数，若分子是代数式，则必加括号。2、去括号去括号法则、乘法分配律严格执行去括号的法则，若是数乘括号，切记不漏乘括号内的项，减号后去括号，括号内各项的符号一定要变号。三、解一元一次方程的步骤：3、移项等式的性质1“越过=”的叫移项，属移项者必变号；未移项的项不变号，注意不遗漏,移项时把含未知数的项移在左边，已知数移在右边，书写时，先写不移动的项，把移动过来的项改变符号写在后面。4、合并同类项合并同类项法则注意在合并时，仅将系数加到了一起，而字母及其指数均不改变。5、系数化为1等式的性质2两边同除以未知数的系数，记住未知数的系数永远是分母（除数），切不可分子、分母颠倒。6、检验（重点要检查，不要功败垂成）检验结果正确性把方程的解带回原方程检验正确性。1.行程问题：路程＝速度×时间2.和差倍分问题：增长量＝原有量×增长率3.利润问题：商品利润＝商品售价－商品进价4.工程问题：工作量＝工作效率×工作时间，各部分劳动量之和＝总量5.银行存贷款问题：本息和＝本金+利息，利息＝本金×利率×期数四、用一元一次方程解决实际问题的常见类型：例题1．下列方程中，哪些是一元一次方程?哪些不是?(1)X2+5+4X=11X；(2)2x+y＝5；(3)x2-5x+6＝0；(4)(2-X)/X=3；(5)．(y-1)/2+y/3=1【思路点拨】若一个整式方程经过化简变形后，只含有一个未知数，并且未知数的次数都是1，系数不为0，则这个方程是一元一次方程．【答案】(1)、(5)是一元一次方程．因为它们或等价变形后是只含有一个未知数、并且未知数的次数是1的方程；(2)、(3)、(4)都不是一元一次方程，因为(2)中含有两个未知数；(3)中未知数的最高次数是2；(4)中分母含有未知数，它不是整式方程．．【典型例题】【变式】下列说法中正确的是().A．2a-a=a不是等式B．x2-2x-3是方程C．方程是等式D．等式是方程。举一反三：【答案】C例题2.若方程3(x-1)+8＝2x+3与方程的解相同，求k的值253xkx解：解方程3(x-1)+8＝2x+3，得x＝-2．将x＝-2代入方程中，得．解这个关于k的方程，得．所以，k的值是．253xkx22253k263k263k【变式】若关于x的方程2(x-1)-a＝0的解是x＝3，则a的值是()．A．4B．-4C．5D．-5举一反三：【答案】A.例题3．解方程【思路点拨】通过方程的同解原理(去分母，去括号，合并同类项，系数化为1)，一步一步将一个复杂的方程转化成与它同解的最简的方程，从而达到求解的目的．235146yy解：去分母，得3(y+2)-2(3-5y)＝12去括号，得3y+6-6+10y＝12合并同类项，得13y＝12未知数的系数化为1，得1213y例题4．(南京)甲车从A地出发以60km／h的速度沿公路匀速行驶，0.5h后，乙车也从A地出发，以80km／h的速度沿该公路与甲车同向匀速行驶，求乙车出发后几小时追上甲车．解：设乙车出发后x小时追上甲车，依题意得60×0.5+60x＝80x，解得x＝1.5．答：乙车出发后1.5小时追上甲车．【总结】此题的等量关系为：甲前0.5h的行程+甲后来的行程＝乙的行程．实战演练:1、下列方程中，是一元一次方程的是（）（A）（B）（C）（D）2、已知等式，则下列等式中不一定成立的是（）ABCD;342xx;0x;12yx.11xx523ba;253ba;6213ba;523bcac.3532baBC3、解方程，去分母得（）（A）（B）（C）（D）2631xx;331xx;336xx;336xx.331xxC4、下列方程变...