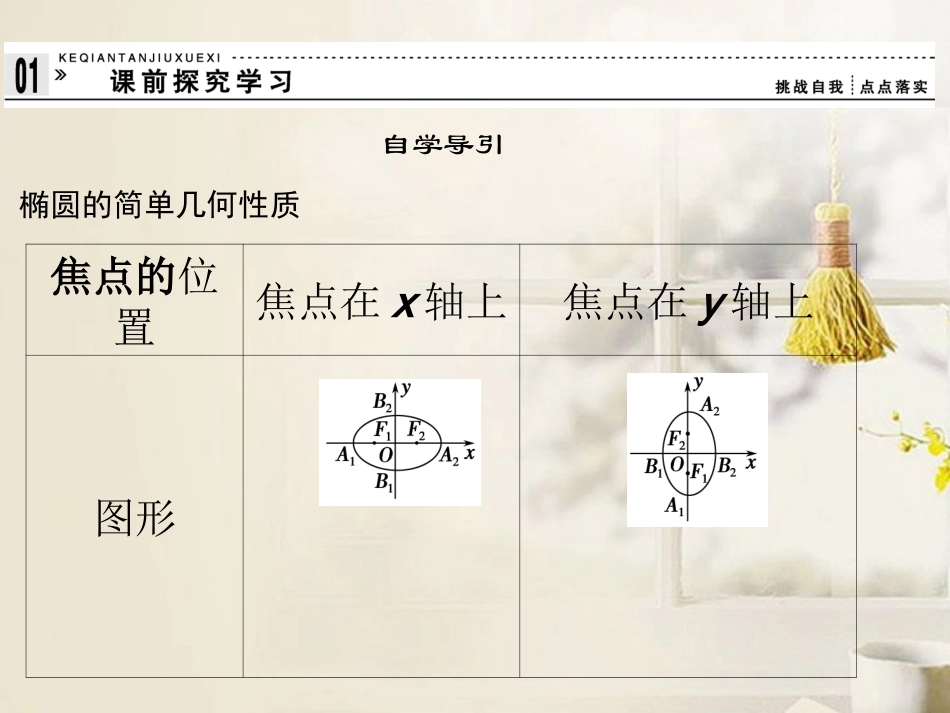
2.1.2椭圆的简单几何性质第1课时椭圆的简单几何性质【课标要求】1.掌握椭圆的简单几何性质.2.理解离心率对椭圆扁平程度的影响.【核心扫描】1.椭圆的简单几何性质.(重点)2.求椭圆的离心率.(难点)3.常结合几何图形、方程、不等式、平面向量等内容命题.自学导引椭圆的简单几何性质焦点的位置焦点在x轴上焦点在y轴上图形(a>b>0)(a>b>0)-a≤x≤a且-b≤y≤b-b≤x≤b且-a≤y≤aA1(-a,0)、A2(a,0)B1(0,-b)、B2(0,b)A1(0,-a)、A2(0,a)B1(-b,0)、B2(b,0)轴长短轴长=,长轴长=焦点焦距|F1F2|=对称性对称轴,对称中心离心率e=ca(0<e<1)2b2aF1(-c,0)、F2(c,0)F1(0,-c)、F2(0,c)2cx轴和y轴(0,0)想一想:能否用a和b表示椭圆的离心率e?222222221ababaacacee名师点睛1.椭圆几何性质的应用(1)椭圆的焦点决定椭圆的位置,范围决定椭圆的大小,离心率决定了椭圆的扁圆程度,对称性是椭圆的重要特征,顶点是椭圆与对称轴的交点,是椭圆重要的特殊点;若已知椭圆的标准方程,则根据a、b的值可确定其性质.(2)明确a,b的几何意义,a是长半轴长,b是短半轴长,不要与长轴长、短轴长混淆,由c2=a2-b2,可得“已知椭圆的四个顶点,求焦点”的几何作图法,只要以短轴的端点B1(或B2)为圆心,以a为半径作弧交长轴于两点,这两点就是焦点.(3)如图所示椭圆中的△OF2B2找出a,b,c,e对应的线段或量为a=|F2B2|,b=|OB2|,c=|OF2|,e=ca=|OF2||F2B2|=cos∠OF2B2.(4)若椭圆的标准方程为x2a2+y2b2=1(a>b>0),则椭圆与x轴的交点A1,A2到焦点F2的距离分别最大和最小,且|A1F2|=a+c,|A2F2|=a-c.题型一由椭圆方程求椭圆的几何性质【例1】求椭圆9x2+16y2=144的长轴长、短轴长、离心率、焦点和顶点坐标.[思路探索]先将椭圆方程化为标准形式,再利用a、b、c之间的关系求解.解已知方程化成标准方程为x216+y29=1,于是a=4,b=3,c=16-9=7,∴椭圆的长轴长和短轴长分别是2a=8和2b=6,离心率e=ca=74,又知焦点在x轴上,∴两个焦点坐标分别是F1(-7,0)和F2(7,0),四个顶点坐标分别是A1(-4,0),A2(4,0),B1(0,-3)和B2(0,3).规律方法解决此类问题的方法是将所给方程先化为标准形式,然后根据方程判断出椭圆的焦点在哪个坐标轴上,再利用a,b,c之间的关系和定义,求椭圆的基本量.【变式1】求椭圆4x2+9y2=36的长轴长和焦距、焦点坐标、顶点坐标和离心率.解将椭圆方程变形为x29+y24=1,∴a=3,b=2,∴c=a2-b2=9-4=5.∴椭圆的长轴长和焦距分别为2a=6,2c=25,焦点坐标为F1(-5,0),F2(5,0),顶点坐标为A1(-3,0),A2(3,0),B1(0,-2),B2(0,2),离心率e=ca=53.题型二由椭圆的几何性质求标准方程【例2】求适合下列条件的椭圆的标准方程:(1)长轴长是10,离心率是45;(2)在x轴上的一个焦点,与短轴两个端点的连线互相垂直,且焦距为6.[思路探索]解答本题可先由已知信息判断焦点所在坐标轴并设出标准方程,再利用待定系数法求参数a,b,c.解(1)设椭圆的方程为x2a2+y2b2=1(a>b>0)或y2a2+x2b2=1(a>b>0).由已知得,2a=10,a=5.e=ca=45,∴c=4.∴b2=a2-c2=25-16=9.∴椭圆的标准方程为x225+y29=1或x29+y225=1.(2)依题意,可设椭圆方程为x2a2+y2b2=1(a>b>0).如图所示,△A1FA2为一等腰直角三角形,OF为斜边A1A2的中线(高),且|OF|=c,|A1A2|=2b,∴c=b=3,∴a2=b2+c2=18,故所求椭圆的方程为x218+y29=1.规律方法利用性质求椭圆的标准方程,通常采用待定系数法,而其关键是根据已知条件确定其标准方程的形式并列出关于参数的关系式,利用解方程(组)求解,同时注意a、b、c、e的内在联系以及对方程两种形式的讨论.【变式2】求满足下列各条件的椭圆的标准方程.(1)已知椭圆的中心在原点,焦点在y轴上,若其离心率为12,焦距为8.(2)短轴一个端点与两焦点组成一个正三角形,且焦点到同侧顶点的距离为3.解(1)由题意知,2c=8,c=4,∴e=ca=4a=12,∴a=8,从而b2=a2-c2=48,∴椭圆方程是y264+x248=1.(2)由已知a=2c,a-c=3,∴a=...