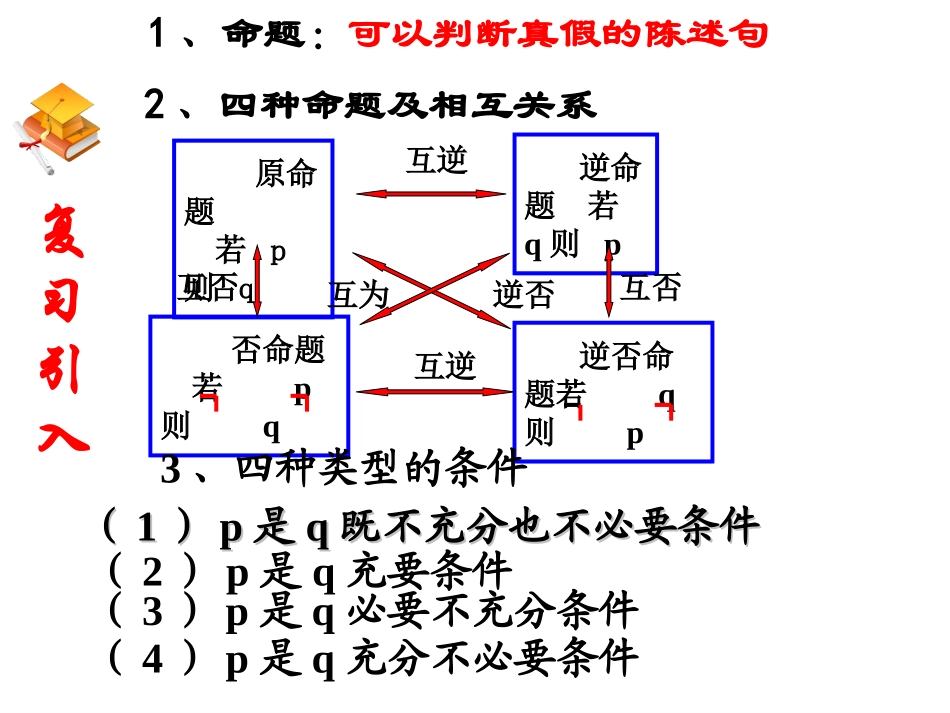
常用逻辑用语知识网络常用逻辑用语命题及其关系简单的逻辑联结词全称量词与存在量词四种命题充分条件与必要条件量词全称量词存在量词含有一个量词的否定或且非并集交集补集运算复习引入1、命题:可以判断真假的陈述句2、四种命题及相互关系原命题若p则q逆命题若q则p否命题若p则q逆否命题若q则p互逆互逆互否互否互为逆否3、四种类型的条件((11))pp是是qq既不充分也不必要条件既不充分也不必要条件(4)p是q充分不必要条件(3)p是q必要不充分条件(2)p是q充要条件1.3简单逻辑连接词且、或、非(1)对“且”的理解,可联想到集合中“交集”的概念.A∩B={x︱x∈A且x∈B}中的“且”,是指“x∈A”、“x∈B”这两个条件都要满足的意思概念(2)对“或”的理解,可联想到集合中“并集”的概念.A∪B={x︱x∈A或x∈B}中的“或”,它是指“x∈A”、“x∈B”中至少一个是成立的,即x∈A且xB;也可以xA且x∈B;也可以x∈A且x∈B.(3)对“非”的理解,可联想到集合中“补集”的概念.且:就是两者都要、都有的意思.或:就是两者至少有一个的意思(可兼有)非:就是否定的意思(3)6不是2的倍数(1)6是2的倍数且6是3的倍数;(2)6是2的倍数或6是3的倍数;或且不非逻辑联结词p或qp且q非p(p的否定)p∧qp∨q∟p读作:记作:考察下列命题:命题p:6是2的倍数;命题q:6是3的倍数;简单命题复合命题思考(真)(真)(真)(真)(假)例1先判断下列简单命题的真假,再分别用“”联结成新命题,最后再判断复合命题的真假。(1)p:函数y=x2是奇函数;q:函数y=x2在定义域上是减函数;(2)p:函数y=sinx是周期函数;q:函数y=sinx在定义域上递减;(3)p:35是15的倍数;q:35是7的倍数;pq:∧函数y=x2是奇函数且在定义域上是减函数。pq:∧函数y=sinx是周期函数且在定义域上递减。pq:35∧是15的倍数且是7的倍数。(假)(假)(假)(假)(真)(假)(真)(假)(假)探究且和或pq:∨函数y=sinx是周期函数或在定义域上递减。pq:∨函数y=x2是奇函数或在定义域上是减函数。pq:35∨是15的倍数且是7的倍数。(假)(真)(真)1.下列说法正确的是()A.命题“2是偶数且2是素数”使用了逻辑联结词“或”B.命题“方程x2=1的解是x=±1”没有使用逻辑联结词C.命题“π不是整数”使用了逻辑联结词“非”D.命题“6≤8”使用了逻辑联结词“且”C练习2.命题p:2{2∈,6},命题q:{1}{1,2}∈,则下列判断正确的是()A.p∨q为真,p∧q为真,非p为假B.p∨q为真,p∧q为假,非p为真C.p∨q为假,p∧q为假,非p为假D.p∨q为真,p∧q为假,非p为假D练习3.在下列命题中(1)命题“不等式没有实数解”;(2)命题“-1是偶数或奇数”;(3)命题“既属于集合,也属于集合”;(4)命题“”其中,真命题为_____________.0|2|x2BAAUQR(2)(4)练习(1)p:若x>y,则5x>5y;(2)q:已知a,b为实数,若x2+ax+b≤0有非空实解集,则a2-4b≥0。4、写出下列命题的否定与它的否命题练习非p:若x>y,则5x≤5yp的否命题:若x≤y,则5x≤5y非q:已知a,b为实数,若x2+ax+b≤0有非空实解集,则a2-4b<0q的否命题:已知a,b为实数,若x2+ax+b≤0没有实数解,则a2-4b<0的值。同时为假命题,求与“且命题::已知命题例xq"p,:q,6xp12qZxx例题∵pq∧为假,“非q”为假∴p为假q为真Zxx32所以x的值分别为-1,0,1,2.解∵x2-x≥6∴x≥3或x≤-2即p:x≥3或x≤-2变式的取值范围。求实数为假命题,为真命题,,)若(的取值范围;的充分条件,求实数是若,(设已知x""""5m2qp)1(22:,0)6)(2x:,0mqpqpmmxmqxp设p:方程x2+mx+1=0有两个不等的负根,q:方程4x2+4(m-2)x+1=0无实根.若p∨q为真,p∧q为假,求m的取值范围.解:∵若方程x2+mx+1=0有两个不等的负根即p:m>2又∵若方程4x2+4(m-2)x+1=0无实根则∆=16(m-2)2-16<0,即1