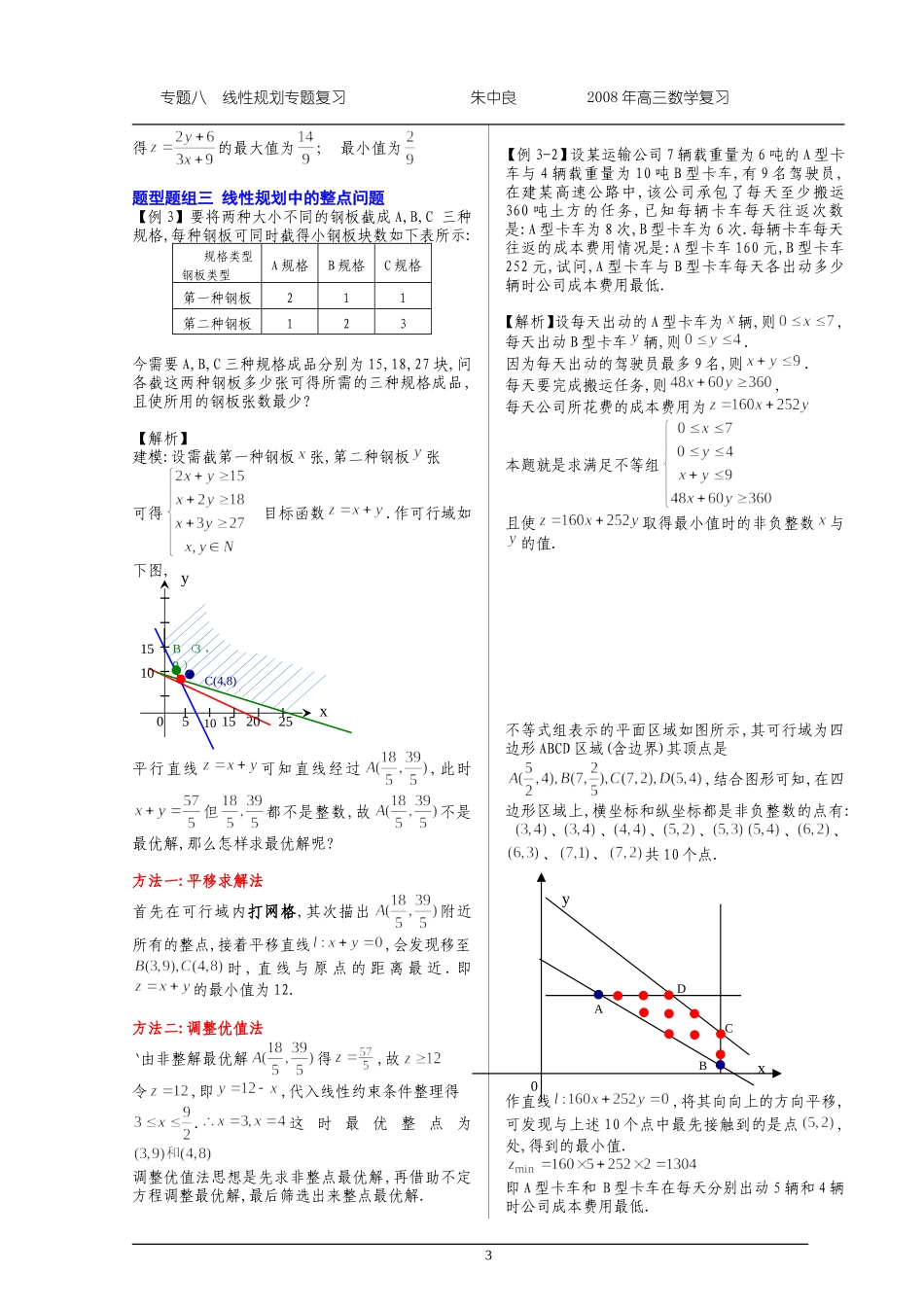
专题八线性规划专题复习朱中良2008年高三数学复习专题八线性规划专题复习蕲春县横车高中朱中良(示范课连堂讲稿多媒体课件)考纲研读了解二元一次不等式所表示的平面区域;了解线性规划的意义,并会简单的应用.基础知识梳理1、二元一次不等式表示平面区域(1)在平面直角坐坐系中,已知直线,坐标平面内的点①若,则点在直线的上方;②若,则点在直线的下方;若等于零,则比较简单.一般情况下,我们可以将一个二元一次不等式化为的形式,则可利用“大于零在上方,小于零在下方”,画出相应的区域.“直线定界,不等式(点)定域”2、线性规划的概念(1)求线性目标函数在线性约束条件下的最大值或最小值的问题,统称为线性规划问题.(2)满足线性约束条件的解叫可行解,由所有可行解组成的集合叫可行域.(3)可行解中使目标函数取得最大值或最小值的解叫做最优解.3、线性规划的应用用解线性规划解应题的一般步骤(1)依题意设出变量,分析并将已知数据列出表格;(2)确定线性约束条件;(3)确定线性目标函数;(4)画出可行域;(5)利用线性目标函数求出最优解;(6)根据实际问题的需要,适当调整最优解(如整数解等).4.规律与方法(1)如果可行域是一个多边形,那么一般在其顶点处使目标函数取得最大值或最小值.最优解一般是多边形的某个顶点,到底是那个顶点为最优解,有两种解定方法:一是将目标函数的直线平行移动,最先通过或最后通过的一个便是;另一种方法是利用围成可行域的直线斜率来判断.特别地,当线性目标函数的直线与可行域某条边平行时,其最优解可能有无组解.(2)求整点的最优解方法①调整优值法,适用于较复杂的问题.②网格法,精确作图,适用于可行域较小的问题.③逐点验证法,可行区域是有限区域且整点个数又较少.三、组型题组教学设计题型题组一线性区域问题【例1】(1)(2005年全国卷)在坐标平面上,不等式组所表示的平面区域面积()A.B.C.D.2【解析】等价于或再画线性可行域(如图所示)于是有故选(B)(2)不等式组所表示的平面区域记为D,则平面区域D的面积为【解析】平面区域D的面积为:(关注:以解析几何、三角中的曲线作为区域边界的非线性约束条件)题型题组二线性规划求最值问题【例2】已知平面内点满足,为坐标原点.请完成下各题(1)若求目标函数的最大值和最小值.1x0yA(0,1)D(0,-1)C(-1,-2)Bx0y2211专题八线性规划专题复习朱中良2008年高三数学复习(2)求目标函数的最大值和最小值.(3)求目标函数的最大值和最小值.(4)求目标函数的最大值和最小值.(5)是否存在实数,使得有无穷多个点,使得目标函数取得最小值,若存在,试求出出的取值,若不存在请说明理由.【直观感觉】目标函数新颖教材中的目标函数的几何意义一般是直线的斜率或截距。这里有“以向量为背景”,有“绝对值目标函数”,有“二次式目标函数”,有“二元一次商式目标函数”等,较复杂。【思路方法】关键抓住目标函数它所赋予的几何意义,这里要求有较强的转化意识和数形结合能力。【解析】(1)易得的最大值为6,最小值为2(2)目标函数是两点间距离公式的型问题转化为先解决的最大值和最小值,它是表示点到的距离的平方。依点到线的距离公式易求得的最小值为的最大值为(3)目标函数是点到线的距离型,也就是目标函数是的形式可以变其它变为,其几何意义是可行域内的点到直线的距离的倍.求得的最小值为的最大值为(4)目标函数是的形式(均不为0)可以将目标函数化为,它表示可行区域内的点与点的连斜率的倍.2x0yA(0,4)C(2,0)B(6,0)x0yA(0,4)C(2,0)B(6,0)x0yA(0,4)C(2,0)B(6,0)x0yA(0,4)C(2,0)B(6,0)x0yA(0,4)C(2,0)B(6,0)D(3,4)专题八线性规划专题复习朱中良2008年高三数学复习得的最大值为;最小值为题型题组三线性规划中的整点问题【例3】要将两种大小不同的钢板截成A,B,C三种规格,每种钢板可同时截得小钢板块数如下表所示:规格类型钢板类型A规格B规格C规格第一种钢板211第二种钢板123今需要A,B,C三种规格成品分别为15,18,27块,问各截这两种钢板多少张可得所需的三种规格成品,且使所用的钢板张数最少?【解析】建模:设需截第一种钢板张,第二种钢板张可得目标函数.作可行域如下图,平行直线可知直线经过,此时但都不是整数,故不是最优解,那么怎样求最优解呢?方法...