椭圆及其标准方程(第一课时)VIP免费

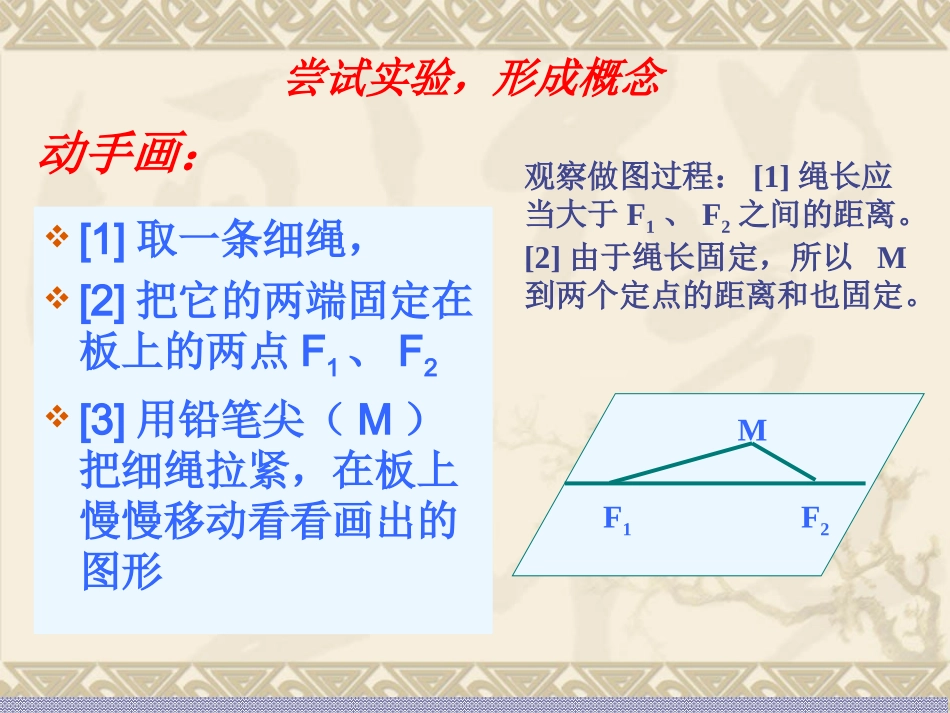
课题：《椭圆及其标准方程》高二数学组生活中的椭圆（一）认识椭圆尝试实验，形成概念[1]取一条细绳，[2]把它的两端固定在板上的两点F1、F2[3]用铅笔尖（M）把细绳拉紧，在板上慢慢移动看看画出的图形F1F2M观察做图过程：[1]绳长应当大于F1、F2之间的距离。[2]由于绳长固定，所以M到两个定点的距离和也固定。动手画：二、概念透析F1F2M平面内到两个定点平面内到两个定点FF11、、FF22的距离的和等于常数的距离的和等于常数（大于（大于|F|F11FF22||））的点的轨迹叫的点的轨迹叫椭圆。椭圆。这两个定点这两个定点FF11、、FF22叫做椭圆的叫做椭圆的焦点焦点两焦点之间的距离叫做两焦点之间的距离叫做焦距。焦距。1、椭圆的定义如果设轨迹上任一点M到两定点FF11、、FF22的距离和为常数2a，两定点之间的距离为2c，则椭圆定义还可以用集合语言表示为：P={M||MF1|+|MF2|=2a（2a>2c）}．（1）平面曲线（2）到两定点F1，F2的距离和等于定长（3）定长﹥|F1F2|反思：椭圆上的点要满足怎样的几何条件？平面内到两个定点平面内到两个定点FF11、、FF22的距离的和等于常数的距离的和等于常数（大于（大于|F|F11FF22||））的点的轨迹叫的点的轨迹叫椭圆。椭圆。这两个定点这两个定点FF11、、FF22叫做椭圆的叫做椭圆的焦点焦点两焦点之间的距离叫做两焦点之间的距离叫做焦距。焦距。注：定长所成曲线是椭圆定长所成曲线是线段定长无法构成图形212121FF2aFF2aFF2a理解定义的内涵和外延一定要准确把握奥！OXYF1F2M三、椭圆方程的建立步骤一：建立直角坐标系,步骤二：设动点坐标步骤三：列方程步骤四：化简方程求曲线方程的步骤:解：取过焦点F1、F2的直线为x轴，线段F1F2的垂直平分线为y轴，建立平面直角坐标系(如图).设M(x,y)是椭圆上任意一点，椭圆的焦距2c(c>0)，M与F1和F2的距离的和等于正常数2a(2a>2c)，则F1、F2的坐标分别是(c,0)、(c,0).（想一想：下面怎样化简？）222221)(||,)(||ycxMFycxMFaycxycx2)()(2222得方程由椭圆的定义，代入坐标OxyMF1F2方程推导：PxyoacbcaOP22||令则方程可化为则方程可化为观察左图，你能从中找出表示观察左图，你能从中找出表示cc、、aa的线段吗？的线段吗？12222byax即即122222cayaxaa22-c-c22有什么几何意义？有什么几何意义？b0ab（）)0(12222babxay012222babyax焦点在y轴：焦点在x轴：2、椭圆的标准方程:1oFyx2FM12yoFFMxF1（-c，0）、F2（c，0）F1（0，-c）、F2（0，c）OXYF1F2M(-c,0)(c,0)YOXF1F2M(0,-c)(0,c))0(12222babyax)0(12222babxay♦椭圆的标准方程的特点：（1）椭圆标准方程的形式：左边是两个分式的平方和，右边是1（2）椭圆的标准方程中三个参数a、b、c满足a2=b2+c2。（3）由椭圆的标准方程可以求出三个参数a、b、c的值。（4）椭圆的标准方程中，x2与y2的分母哪一个大，则焦点在哪一个轴上。22221.153xy，则a＝，b＝；则a＝，b＝；22222.146xy，则a＝，b＝；则a＝，b＝；55334466口答：则a＝，b＝；则a＝，b＝；则a＝，b＝．则a＝，b＝．337169.322yx6147.422yx211625)1(22yx）不等于其中0(11)4(2222mmymx123)3(22yx分母哪个大，焦点就在哪个坐标轴上，反之亦然。注意：（四）尝试应用1、下列方程哪些表示的是椭圆，如果是，判断它的焦点在哪个坐标轴上？0225259)2(22yx变式一:将上题焦点改为(0，-4)、(0，4)，结果如何？192522xy变式二变式二::将上题改为两个焦点的距离为8，椭圆上一点P到两焦点的距离和等于10，结果如何？192522yx192522xy已知两个焦点的坐标分别是(-4,0)、(4,0)，椭圆上一点P到两焦点距离的和等于10；221259xy2、写出适合下列条件的椭圆的标准方程当焦点在X轴时，方程为：当焦点在Y轴时，方程为：３.求下列椭圆的焦点坐标，以及椭圆上每一点到两焦点距离的和。14)1(22yx154)2(22yx434)3(22yx解：椭圆方程具有形式12222byax其中1,2ba因此31422bac两焦点坐标为)0,3(),0,3(椭圆上每一点到两焦点的距离之和为42a2222+=1>>0xyabab2222+=1>>0xyabba分母哪个大，焦点就在哪个轴上12-,0,0，FcFc120,-0,，FcFc标准方程相同点焦点位置的判断不同点图形焦点坐标探究定义a、b、c的关系xyF1F2MOxyF1F2MOa2-c2=b2(a>b>0)（七）知识整理，形成系统P={M||MF1|+|MF2|=2a（2a>2c）}．