九年级圆周角课件VIP免费

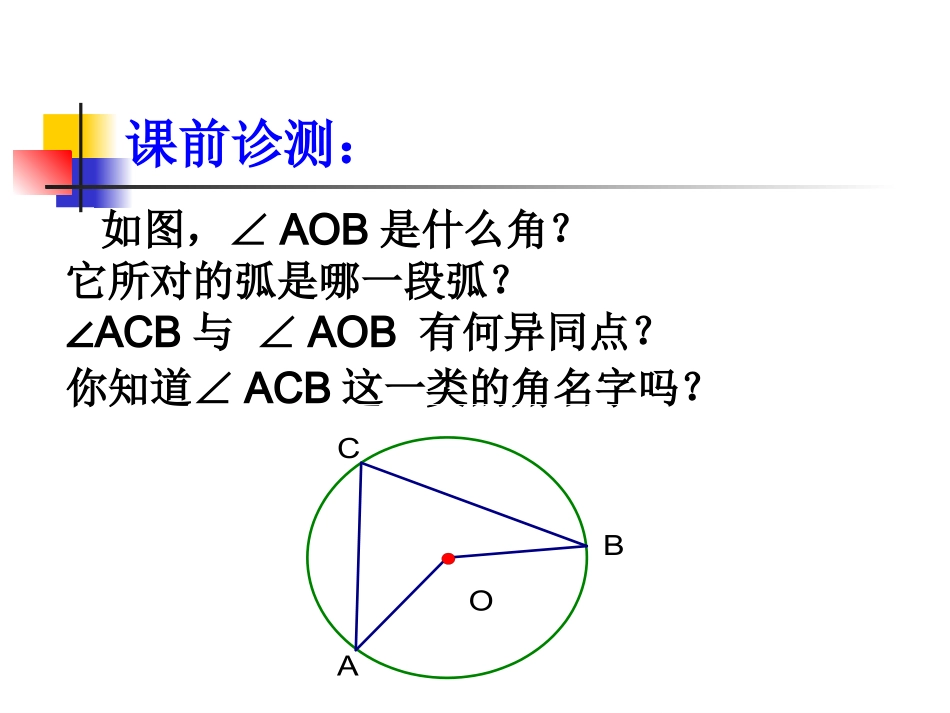
五龙口二中如图，∠AOB是什么角？它所对的弧是哪一段弧？∠ACB与∠AOB有何异同点？你知道∠ACB这一类的角名字吗？课前诊测：BACO圆周角的概念:顶点在圆上两边都与圆相交这样的角叫圆周角火眼金睛：判断下列图形中所画的∠P是否为圆周角？并说明理由。PPPP不是是不是不是顶点不在圆上。顶点在圆上，两边和圆相交。两边不和圆相交。有一边和圆不相交。动手操作：画一画:任意画一个⊙O，画出弧AB所对的圆心角∠AOB；圆周角∠ACB和∠ADB。BOADC动手操作：量一量：分别量出弧AB所对的圆周角∠ACB和∠ADB与∠AOB的度数，并猜想它们之间的关系。说一说：小组交流。想一想：归纳。解决问题：你能证明你的发现（即同弧所对的圆周角度数等于这条弧所对的圆心角的一半）吗？你能画出同弧所对的圆周角和圆心角吗？ABCOABCOABCO分析论证：1.首先考虑一种特殊情况：当圆心(O)在圆周角(∠BAC)的一边(BA)上时,圆周角∠BAC与圆心角∠BOC的大小关系.ABCO∵证明OA=OC∴∠A=C∠又∠BOC=A∠＋∠C∴∠BOC=2A∠∠即A=BOC∠21分析论证：你能证明第2种情况吗？12BADBODABCO提示：作射线AO交⊙O于D。转化为第1种情况D12DACDOC1()2BADDACBODDOC12BACBOC分析论证：你能证明第3种情况吗？12BADBOD提示：作射线AO交⊙O于点D。ABCOD12DACDOC1()2DACDABDOCDOB12BACBOC圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半。课堂反馈：练习：如图，点A、B、C、D在同一个圆上，四边形ABCD的对角线把4个内角分成8个角，这些角中哪些是相等的角？D12345678ABC∠1=4∠∠5=8∠∠2=7∠∠3=6∠问题1：如图，AB是⊙O的直径，请问：∠C1、∠C2、∠C3的度数是。ABOC1C2C3推论：半圆（或直径）所对的圆周角是直角；90°的圆周角所对的弦是直径。问题2：若∠C1、∠C2、∠C3是直角，那么弦AB是。探究与思考：90°直径在同圆或等圆中，如果两个圆周角相等，它们所对弧一定相等吗？为什么？在同圆或等圆中，如果两个圆周角相等，它们所对的弧一定相等．问题3：探究与思考：练一练：1、如图，在⊙O中，∠ABC=50°，则∠AOC等于（）A、50°；B、80°；C、90°；D、100°ACBOD2、如图，△ABC是等边三角形，动点P在圆周的劣弧AB上，且不与A、B重合，则∠BPC等于（）A、30°；B、60°；C、90°；D、45°CABPB练一练：3、如图，∠A=50°，∠ABC=60°BD是⊙O的直径，则∠AEB等于（）A、70°；B、110°；C、90°；D、120°B4、如图，△ABC的顶点A、B、C都在⊙O上，∠C＝30°，AB＝2，则⊙O的半径是。ACBODECABO25、如图，⊙O直径AB为10cm，弦AC为6cm，∠ACB的平分线交⊙O于D，求BC、AD、BD的长．86102222ACABBC又在Rt△ABD中，AD2+BD2=AB2，221052(cm)22ADBDAB解：∵AB是直径，∴∠ACB=∠ADB=90°．在Rt△ABC中，∵CD平分∠ACB，∴AD=BD..ACDBCDOABCD练一练：课后小结：圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半。推论：半圆或直径所对的圆周角是直角，90°的圆周角所对的弦是直径。推论：在同圆或等圆中，如果两个圆周角相等，它们所对的弧一定相等。课后作业：P87练习：2、3.P87复习巩固：2、3、4.