27.2.1-相似三角形的判定-(2)VIP免费

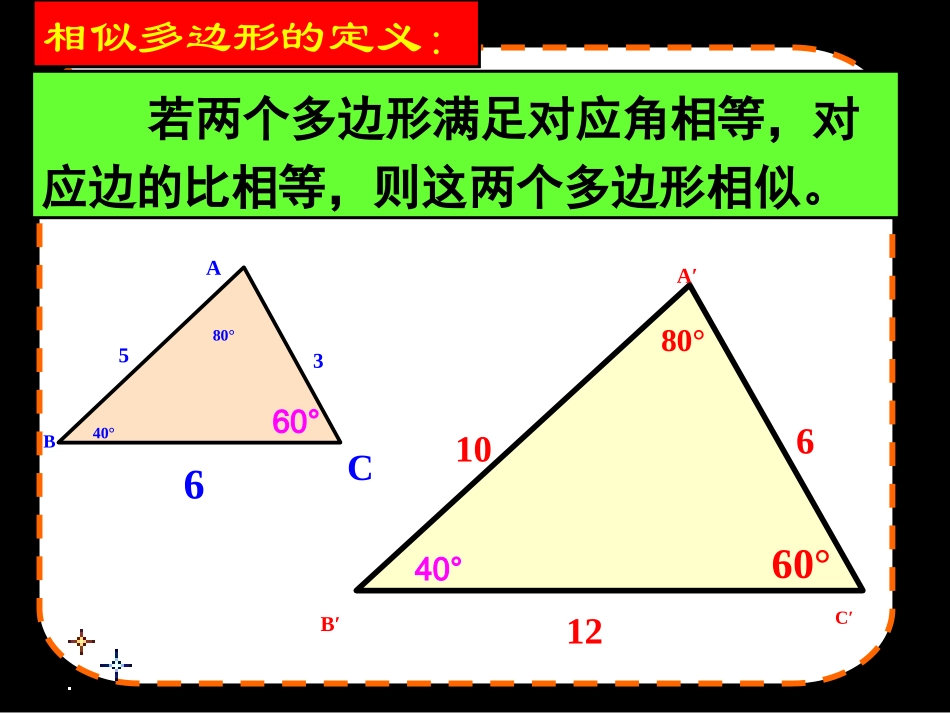
复习提问：问题1：三角形全等的定义与判定方法？三角形全等的定义：三组对应角相等，三组对应边相等。问题2：我们如何判定两个三角形相似？判定方法：SSS、SAS、ASA、AAS、HL（适合于直角三角形）A′B′C′1061260°80°它们是相似三角形吗？为什么？A6BC5380°40°6若两个多边形满足对应角相等，对应边的比相等，则这两个多边形相似。相似多边形的定义：40°60°相似的记法相似的记法“∽”为相似符号，读作“相似于”。CA′ABB′C′若△ABC与△A`B`C`相似则记为△ABCA`B`C`∽△读做“△ABC相似于△A`B`C`”•提问：ABCA′B′C′问题:判定两个三角形相似需要知道这两个三角形三组对应角相等，三组对应边的比相等，能否有更简单的判定方法呢？2如图,DE//BC,且D是边AB的中点,DE交AC于E。3ABCDE问题1：△ADE与△ABC的三组对应角、三组对应边的比各有什么关系？问题2：△ADE与△ABC有什么关系?探究课本P42-43页2如图,DE//BC,且D是边AB的中点,DE交AC于E,ADE△与△ABC有什么关系?说明理由.F1EF∥AB3DE//BCDE=BF，∠A=A∠，∠B=3∠，∠C=2∠在BFED中ABCDEAD=EF，12ADDBAB∵又∠A=1∠，∠2=∠C，△CEFEAD≌△12AEECAC12DEFCBFBC∴△ADE∽△ABC两个三角形的对应边的比有什么关系？12ADAEDEABACBCDB=EF，两个三角形的对应角有什么关系？ABCDED′E′D′E′如图，△ABC中，DEBC,∥若点D是AB的中点，△ADE与△ABC相似。如图，△ABC中，D′E′BC,∥若点D′是AD的中点，△AD′E′与△ABC还会相似吗?相似比是多少？若点D′是AD的四等分点呢？讨讨论论如图，△ABC中，DEBC,∥若点D不是AB的中点，△ADE与△ABC还会相似吗?ABCDE△ADE与△ABC仍相似.“A”型“X”型（图2）DEABCBCADE（图1）判定三角形相似定理：平行于三角形一边的直线与其它两边(或两边延长线)相交,所得的三角形与原三角形相似。ABCDE∵DEBC∥∴△ADEABC∽△几何语言描述：练习练习1、下列各图都满足DEB∥C，是否都有△ADEABC∽△？相似相似相似相似2、如图，在△ABC中，DGEHFI∥∥BC∥，如果AD=1，DB=3，那么DG：BC=_____。ABCDEFGHI1：43、如图,已知DEBC,AE=40cm,EC=20cm,∥BC=48cm,A=45∠0,C=40∠0.(1)求∠1和∠2的大小;(2)求DE的长.ADBEC4504004001295040cm20cm48cm∴DE=32cm406048DE∵DE//BC∴△ADEABC∽△AEDEACBC∴例如：画一个三角形使边长为：1cm、2cm、2.5cm，再画一个三角形，使它的各边长都是这个三角形各边长的2或3倍。探究探究11相似请观察两个三角形的三组对应边有什么特点？相似三角形判定定理：如果两个三角形的三组对应边的比相等，那么这两个三角形相似。任画一个三角形，再画一个三角形，使它的各边长都是原来三角形各边长的k倍(任确定一个倍数)，度量两个三角形的对应角，它们相等吗？这样的两个三角形相似吗？在线段A`B`上截取A`D=AB过点D作DE∥B`C`，交A`C`于点E.已知:如图△ABC和△A`B`C`中求证:△ABC∽△A`B`C`DA`B`C`EBCA''''''ABBCACABBCAC分析：△A`DEA`B`C`∽△''''''''ADDEAEABBCAC''''''ABBCACABBCAC∵A`D=AB同理：DE=BCA`E=AC△A`DE≌ABC△△ABCA`B`C`∽△'''''AEACACAC∴BCA相似三角形判定定理：如果两个三角形的三组对应边的比相等，那么这两个三角形相似。BCAA`B`C`几何语言描述：ABCA`B`C`∴△ABCA`B`C`∽△``````CBBCCAACBAAB∵反馈练习1、试判定△ABC与A′B′C′是否相似，并说明理由．在△ABC和△A′B′C′中，已知：(1)AB＝6cm，BC＝8cm，AC＝10cm，A′B′＝18cm，B′C′＝24cm，A′C′＝30cm．相似，因为对应边的比相等.(2)AB=12cm，BC=15cm，AC＝24cmA′B′＝16cm，B′C′＝20cm，A′C′＝30cm反馈练习试判定△ABC与A′B′C′是否相似，并说明理由．在△ABC和△A′B′C′中，已知：不相似，因为对应边的比不相等.，如图已知AEACDEBCADAB求证：∠1=∠2ADCEB123证明:又∵∠3是公共角∴△ABCADE∽△∴∠BAC=DAE∠ABBCACADDEAE∵∴∠BAC-3=DAE-3∠∠∠∴∠1=2∠2、“A”型“X”型（图2）DEABCBCADE（图1）判定三角形相似定理：平行于三角形一边的直线与其它两边(或两边延长线)相交,所得的三角形与原三角形相似。小结：相似三角形判定定理：如果两个三角形的三组对应边的比相等，那么这两个三角形相似。BCAA`B`C`DE作业：课本：习题27.22（1）、3（1）、5选做题：练习册相应练习说明理由。似比；如果不相似，请似，求出相，它们相似吗？如果相和的正方形网格上有如图在边长为222111A1CBACB不经历风雨，怎么见彩虹没有人能随随便便成功!