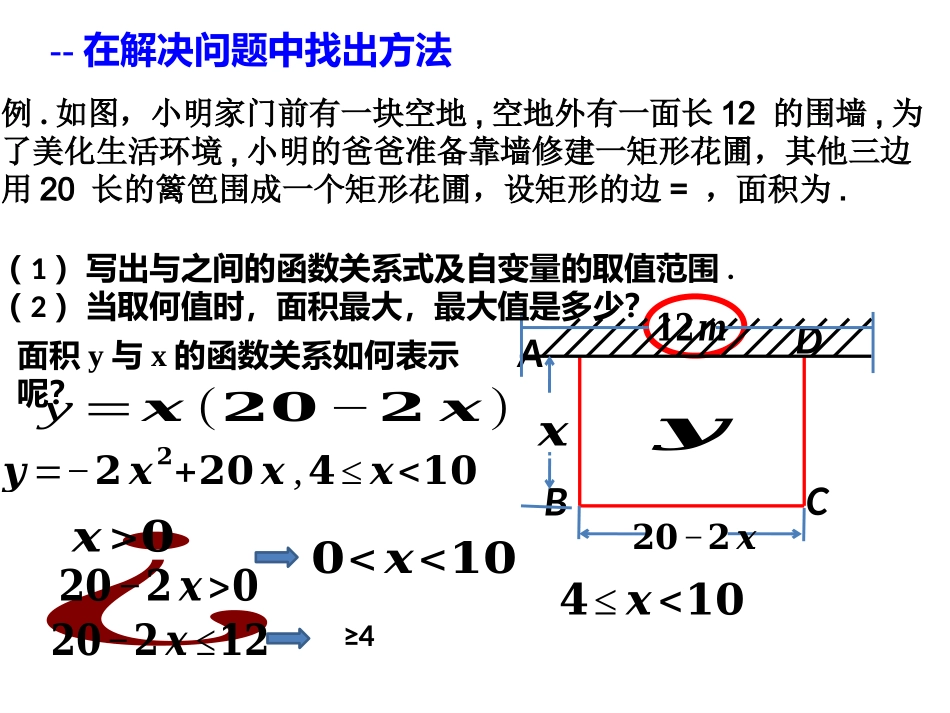
21.4二次函数的应用(最值问题)如何取得最大面积?阜南县第一初级中学丁振云沪科版九年级(上)初中数学例.如图,小明家门前有一块空地,空地外有一面长12的围墙,为了美化生活环境,小明的爸爸准备靠墙修建一矩形花圃,其他三边用20长的篱笆围成一个矩形花圃,设矩形的边=,面积为.面积y与x的函数关系如何表示呢?--在解决问题中找出方法CBADy=𝒙(𝟐𝟎−𝟐𝒙)𝟏𝟐𝒎𝟐𝟎−𝟐𝒙𝒙¿𝟒≤𝒙<𝟏𝟎𝟎<𝒙<𝟏𝟎≥4𝟐𝟎−𝟐𝒙>𝟎𝟐𝟎−𝟐𝒙≤𝟏𝟐𝒙>𝟎𝒚𝒚=−𝟐𝒙𝟐+𝟐𝟎𝒙,𝟒≤𝒙<𝟏𝟎(1)写出与之间的函数关系式及自变量的取值范围.(2)当取何值时,面积最大,最大值是多少?最大面积=?𝒚=−𝟐𝒙𝟐+𝟐𝟎𝒙,𝟒≤𝒙<𝟏𝟎当𝒚=−𝟐(𝒙−𝟓)𝟐+𝟓𝟎50410𝑥=5𝒚=−𝟐𝒙𝟐+𝟐𝟎𝒙O𝒙𝒚𝟒≤𝒙<𝟏𝟎550--在解决问题中找出方法练习.(安徽省2015年中考题)为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为80米的围网在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长度为x米,矩形区域的面积为平方米。(1)求与之间的函数关系式,并注明自变量的取值范围;(2)为何值时,有最大值?最大值是多少?∵三块矩形区域的面积相等,∴矩形AEFD面积是矩形BCFE面积的2倍,∴AE=2BE,设BE=a,则AE=2a,∴8a+2x=80,∴a=-+10,2a=-+20,y=(−12𝑥+20)𝑥+(−14𝑥+10)𝑥a=x+10﹣>0,0<𝑥<40=0<𝑥<40(2)𝑦=−34𝑥2+30𝑥当(1)==最大面积=?𝒚=−𝟐𝒙𝟐+𝟐𝟎𝒙,𝟒≤𝒙<𝟏𝟎当𝒚=−𝟐(𝒙−𝟓)𝟐+𝟓𝟎50410𝑥=5𝒚=−𝟐𝒙𝟐+𝟐𝟎𝒙O𝒙𝒚𝟒≤𝒙<𝟏𝟎谢谢收看!录制单位:阜南县第一初级中学制作教师:丁振云录制时间:2018年5月