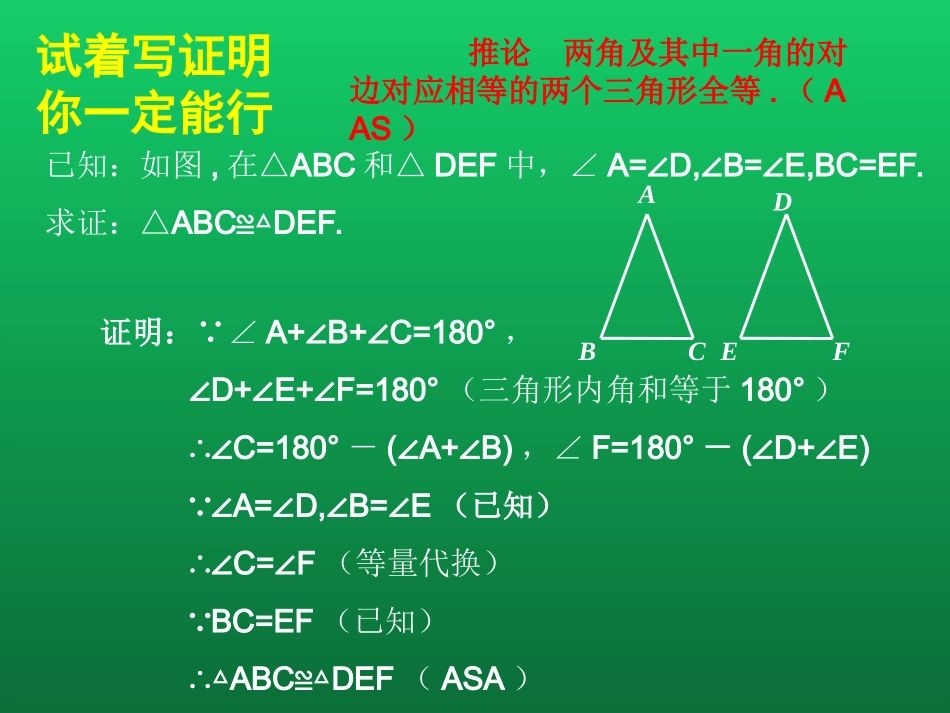
九资河中学周和国1._____对应相等的两个三角形全等;(SSS)2.____________对应相等的两个三角形全等;(SAS)3.____________对应相等的两个三角形全等;(ASA)4.在两个直角三角形中,____________对应相等的两个三角形全等.(HL)5.你能证明下面的推论吗?推论两角及其中一角的对边对应相等的两个三角形全等;(AAS)全等三角形判定定理:两边及其夹角两角及其夹边三边斜边及其一条直角边试着写证明你一定能行推论两角及其中一角的对边对应相等的两个三角形全等.(AAS)已知:如图,在△ABC和△DEF中,∠A=D,B=E,BC=EF.∠∠∠求证:△ABCDEF.≌△证明:∵∠A+B+C=180°∠∠,∠D+E+F=180°∠∠(三角形内角和等于180°)∴∠C=180°-(A+B)∠∠,∠F=180°-(D+E)∠∠∵∠A=D,B=E∠∠∠(已知)∴∠C=F∠(等量代换)∵BC=EF(已知)∴△ABCDEF≌△(ASA)FEDCBA动手做一做,发现了什么准备一个等腰三角形,按如图步骤,先自己折纸观察探索等腰三角形中线段、角的关系,写出你的发现,然后再小组交流,互相弥补不足.→→DCBADCBAD(C)BA等腰三角形顶角的平分线、底边上的中线、底边上的高互相重合.(三线合一)猜想:等腰三角形的性质等腰三角形的两个底角相等.(等边对等角)已知:如图,在△ABC中,AB=AC.求证:∠B=∠C.证明:取BC的中点D,连接AD.在△ABD和△ACD中∵AB=AC,BD=CD,AD=AD∴△ABDACD(SSS)≌△∴∠B=∠C(全等三角形的对应角相等)CBAD证法一:验证猜想,科学证明等腰三角形的两个底角相等.(等边对等角)思考:底边BC上的中线AD是顶角平分线、底边上的高吗?已知:如图,在△ABC中,AB=AC.求证:∠B=∠C.证明:作△ABC顶角∠A的角平分线AD.在△ABD和△ACD中∵AB=AC,∠BAD=∠CAD,AD=AD∴△ABDACD(SAS)≌△∴∠B=∠C(全等三角形的对应角相等)CBAD证法二:等腰三角形的两个底角相等.(等边对等角)思考:顶角平分线AD是底边BC上的中线、底边上的高吗?已知:如图,在△ABC中,AB=AC.求证:∠B=∠C.证明:作边BC上的高AD在RtAB△D和RtAC△D中∵AB=AC,BD=CD,∴△ABDAC≌△D(HL)∴∠B=∠C(全等三角形的对应角相等)CBA证法三:等腰三角形的两个底角相等.(等边对等角)D思考:底边BC上的高AD是顶角平分线、底边上的中线吗?归纳总结,得出结论CBAD在上面的证明过程中,你概括一下线段AD在等腰△ABC中有几种身份?由此你能得到什么结论?推论:等腰三角形顶角的平分线、底边上的中线、底边上的高互相重合.(三线合一)定理:等腰三角形的两个底角相等.(等边对等角)1.等腰三角形的两个底角相等;2.等腰三角形顶角的平分线、底边中线、底边上高三条线重合;等腰三角形的性质如图,在△ABD中,C是BD上的一点,且ACBD⊥,AB=AC,AC=CD,(1)求证:AC=BC;(2)求∠BAD的度数.BCDA你有几种证明方法,请与同学们分享拿出一张纸对折,在折痕上取两点A、D,在重叠部分任取一点M,用剪刀将纸沿AM、DM剪开得△AMD,将△AMD展开(点M分别表示为B、C)探究所得图形是什么图形,可能是三角形吗?如果是,是什么三角形,是在什么条件下?剪纸探秘,我来揭底一般是四边形,可能是等腰三角形,当MDAD⊥时,B、C在一条直线上,满足“三线合一”。2.通过折纸活动获得了猜想,并给予了严格的证明,为今后解决有关等腰三角形的问题提供了丰富的理论依据.3.体会了证明一个命题的严格的要求,体会了证明的必要性课堂小结,畅谈收获:1.等腰三角形的性质(1).等腰三角形的两个底角相等;(2).等腰三角形顶角的平分线、底边中线、底边上高三条线重合;