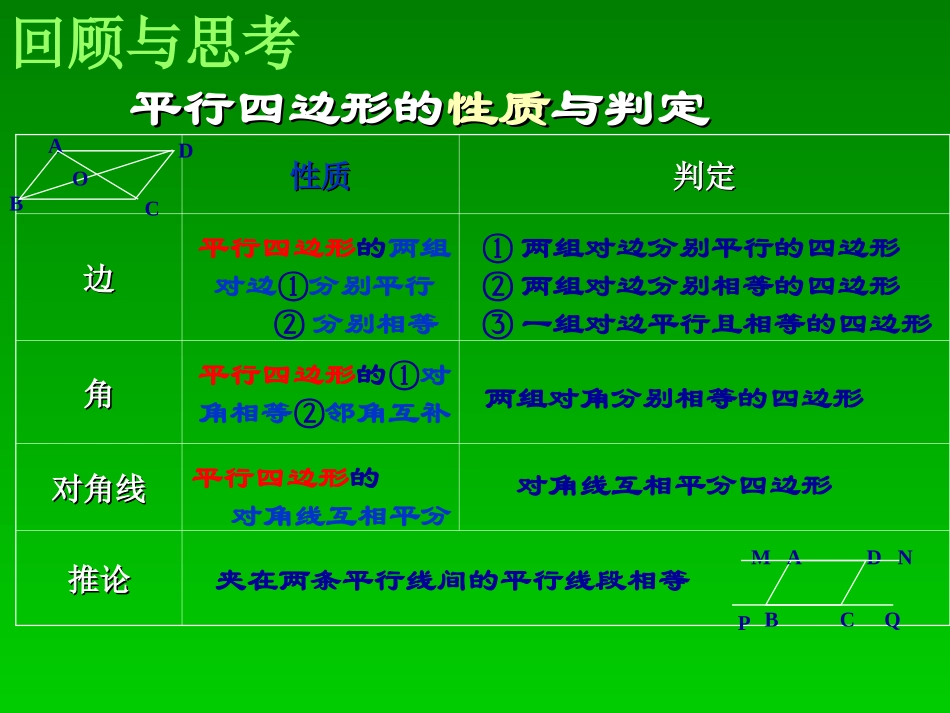
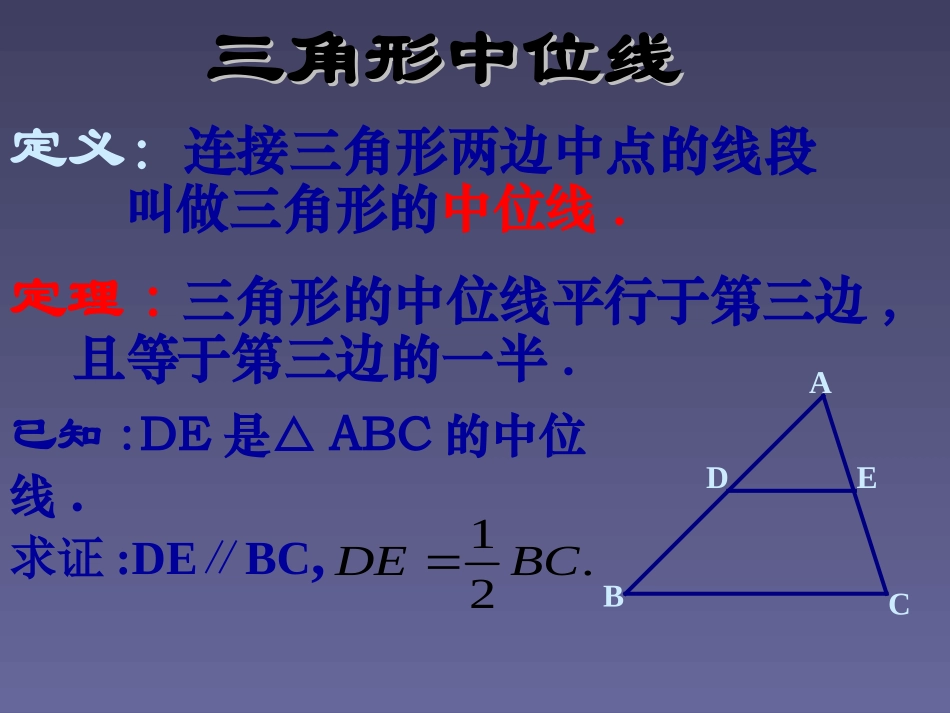
证明三证明三三角形的中位线定理三角形的中位线定理纪达中学黄俏辉平行四边形的平行四边形的性质性质与判定与判定性质性质判定判定边边角角对角线对角线推论推论平行四边形的两组对边①分别平行②分别相等平行四边形的①对角相等②邻角互补平行四边形的对角线互相平分夹在两条平行线间的平行线段相等①两组对边分别平行的四边形②两组对边分别相等的四边形③一组对边平行且相等的四边形两组对角分别相等的四边形对角线互相平分四边形BDCAOBDCAMNPQ回顾与思考三角形中位线三角形中位线定理:三角形的中位线平行于第三边,且等于第三边的一半.已知:DE是△ABC的中位线.DEBCA.21BCDE求证:DEBC∥,定义:连接三角形两边中点的线段叫做三角形的中位线.三角形中位线的性质定理三角形中位线的性质定理证明:如图,延长DE至F,使EF=DE,连接CF.∵AE=CE,∠AED=∠CEF,EF=DE∴△ADE≌△CFE(SAS).∴AD=CF,∠ADE=∠F.∴BD∥CF.∵AD=BD,∴BD=CF,DEBCAF∴四边形DBCF是平行四边形.∴DF∥BC,DF=BC..2121BCDFDE∴DE∥BC,又∵BD∥CF.分割三角形分割三角形你能将任意一个三角形分成四个全等的三角形吗?BCAD··E·F做一做1已知:如图,D,E,F分别是△ABC各边的中点.求证:△ADE≌△DBF≌△EFC≌△FED.做一做做一做22如图:任意作一个四边形,并将其四边的中点依次连接起来,得到一个新的四边形,这个四边形的形状有什么特征?请证明你的结论。ABCDEFGH分析:连接AC,将四边形分割成两个三角形,应用中位线定理证明。证明:连接AC.∵E,F,G,H分别为各边的中点∴EF∥HG,EF=HG.ABCHDEFG任意四边形ABCD各边中点的连线都是平行四边形..21ACEF∴EF∥AC,HG∥AC,.21ACHG∴四边形EFGH是平行四边形.随堂练习随堂练习11如图:A、B两地被池塘隔开,在没有任何测量工具的情况下,小明通过下面的方法估测出A,B间的距离:先在AB外选一点C,然后步测出AC,BC的中点M,N,并测出MN的长,由此他就知道了A,B间的距离。你能说出其中的道理吗?ACBNM已知:在△ABC中,D,E,F分别是边BC,CA,AB的中点.求证:四边形AFDE是平行四边形,它的周长等于AB+AC.ACFBED习题3.31求证:三角形的一条中位线与第三边上的中线互相平分.ACFBED习题习题3.323.32已知:三角形各边长分别8cm,10cm和12cm.求以各边中点为顶点的三角形的周长.ACFBEDP94习题3.33已知:在四边形ABCD中,E,F,G,H分别是边AB,CD,AC,BD的中点.求证:四边形EGFH是平行四边形.DCBGAFHE习题3.34