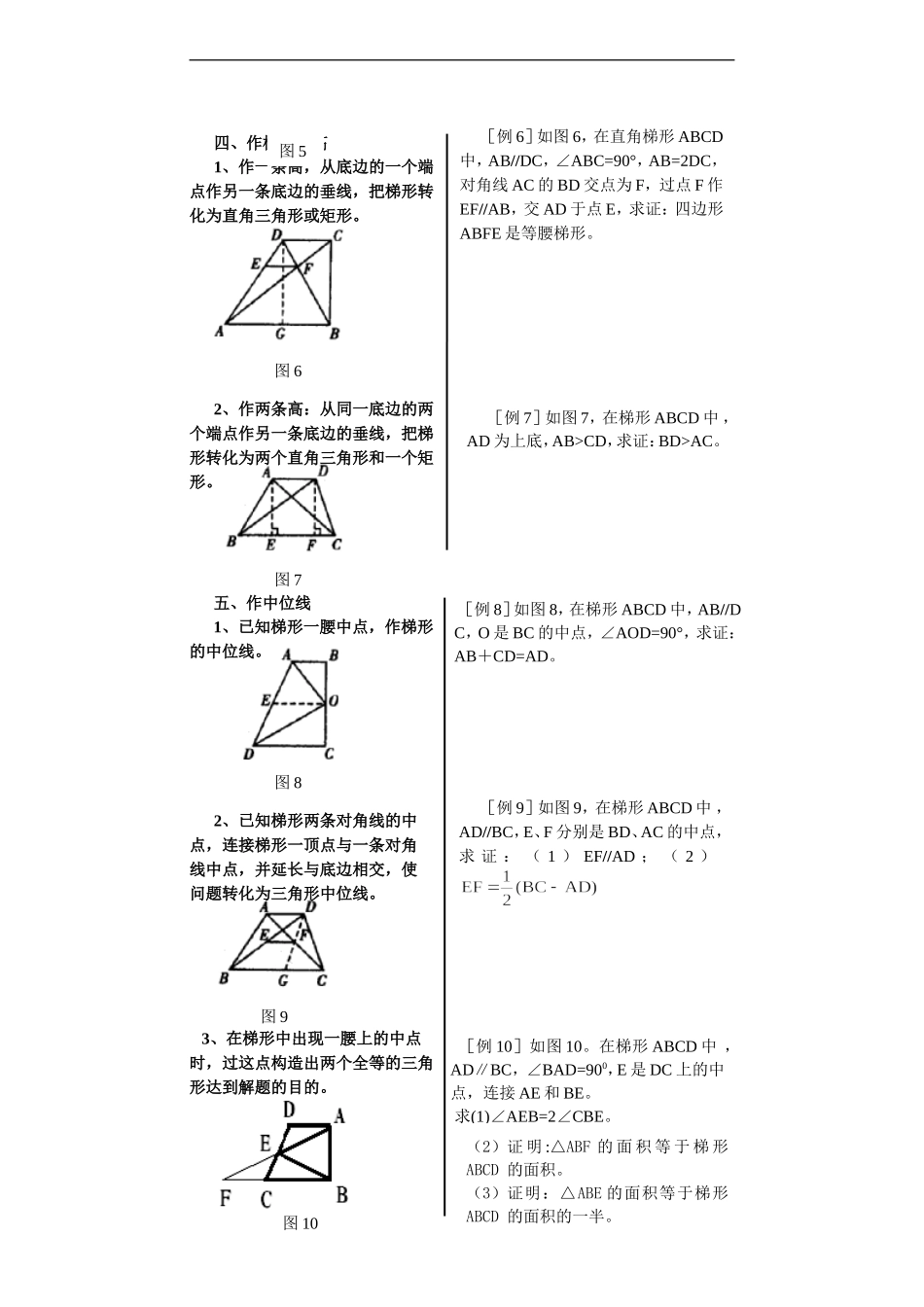
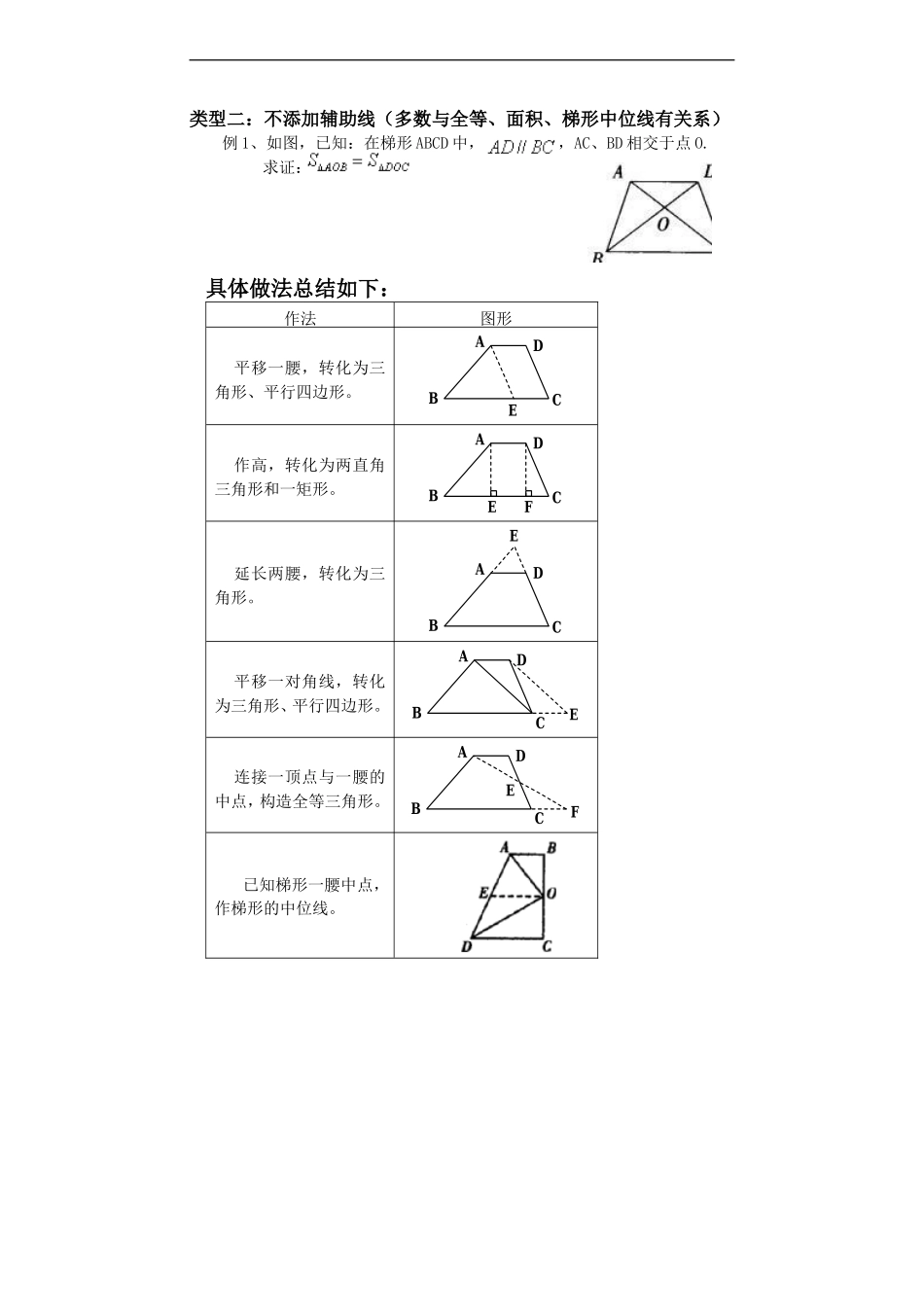
[例4]如图4,在梯形ABCD中,AD//BC,∠B=50°,∠C=80°,AD=2,BC=5,求CD的长。[例3]如图3,在等腰梯形ABCD中,AD//BC,AD=3,BC=7,BD=,求证:AC⊥BD。[例2]如图2,在梯形ABCD中,AD//BC,∠B+∠C=90°,AD=1,BC=3,E、F分别是AD、BC的中点,连接EF,求EF的[例1]如图1,梯形ABCD的上底AB=3,下底CD=8,腰AD=4,求另一腰BC的取值范围。梯形中的常用辅助线在解(证)有关梯形的问题时,常常要添作辅助线,把梯形问题转化为三角形或平行四边形问题。本文举例谈谈梯形中的常用辅助线,以帮助同学们更好地理解和运用。一、平移1、平移一腰:从梯形的一个顶点作一腰的平行线,把梯形转化为一个三角形和一个平行四边形。(如下图)2、平移两腰:利用梯形中的某个特殊点,过此点作两腰的平行线,把两腰转化到同一个三角形中。3、平移对角线:过梯形的一个顶点作对角线的平行线,将已知条件转化到一个三角形中。二、延长即延长两腰相交于一点,可使梯形转化为三角形。三、作对角线即通过作对角线,使梯形转化为三角形。图1图2图3图4[例5]如图5,在直角梯形ABCD中,AD//BC,AB⊥AD,BC=CD,BE⊥CD于点E,求证:AD=DE。(2)证明:△ABF的面积等于梯形ABCD的面积。(3)证明:△ABE的面积等于梯形ABCD的面积的一半。[例10]如图10。在梯形ABCD中,AD∥BC,∠BAD=900,E是DC上的中点,连接AE和BE。求(1)∠AEB=2∠CBE。[例9]如图9,在梯形ABCD中,AD//BC,E、F分别是BD、AC的中点,求证:(1)EF//AD;(2)[例8]如图8,在梯形ABCD中,AB//DC,O是BC的中点,∠AOD=90°,求证:AB+CD=AD。[例7]如图7,在梯形ABCD中,AD为上底,AB>CD,求证:BD>AC。图6[例6]如图6,在直角梯形ABCD中,AB//DC,∠ABC=90°,AB=2DC,对角线AC的BD交点为F,过点F作EF//AB,交AD于点E,求证:四边形ABFE是等腰梯形。图7图8图9图10四、作梯形的高1、作一条高,从底边的一个端点作另一条底边的垂线,把梯形转化为直角三角形或矩形。2、作两条高:从同一底边的两个端点作另一条底边的垂线,把梯形转化为两个直角三角形和一个矩形。五、作中位线1、已知梯形一腰中点,作梯形的中位线。2、已知梯形两条对角线的中点,连接梯形一顶点与一条对角线中点,并延长与底边相交,使问题转化为三角形中位线。3、在梯形中出现一腰上的中点时,过这点构造出两个全等的三角形达到解题的目的。图5类型二:不添加辅助线(多数与全等、面积、梯形中位线有关系)例1、如图,已知:在梯形ABCD中,,AC、BD相交于点O.求证:具体做法总结如下:作法图形平移一腰,转化为三角形、平行四边形。ABCDE作高,转化为两直角三角形和一矩形。ABCDEF延长两腰,转化为三角形。ABCDE平移一对角线,转化为三角形、平行四边形。ABCDE连接一顶点与一腰的中点,构造全等三角形。ABCDEF已知梯形一腰中点,作梯形的中位线。