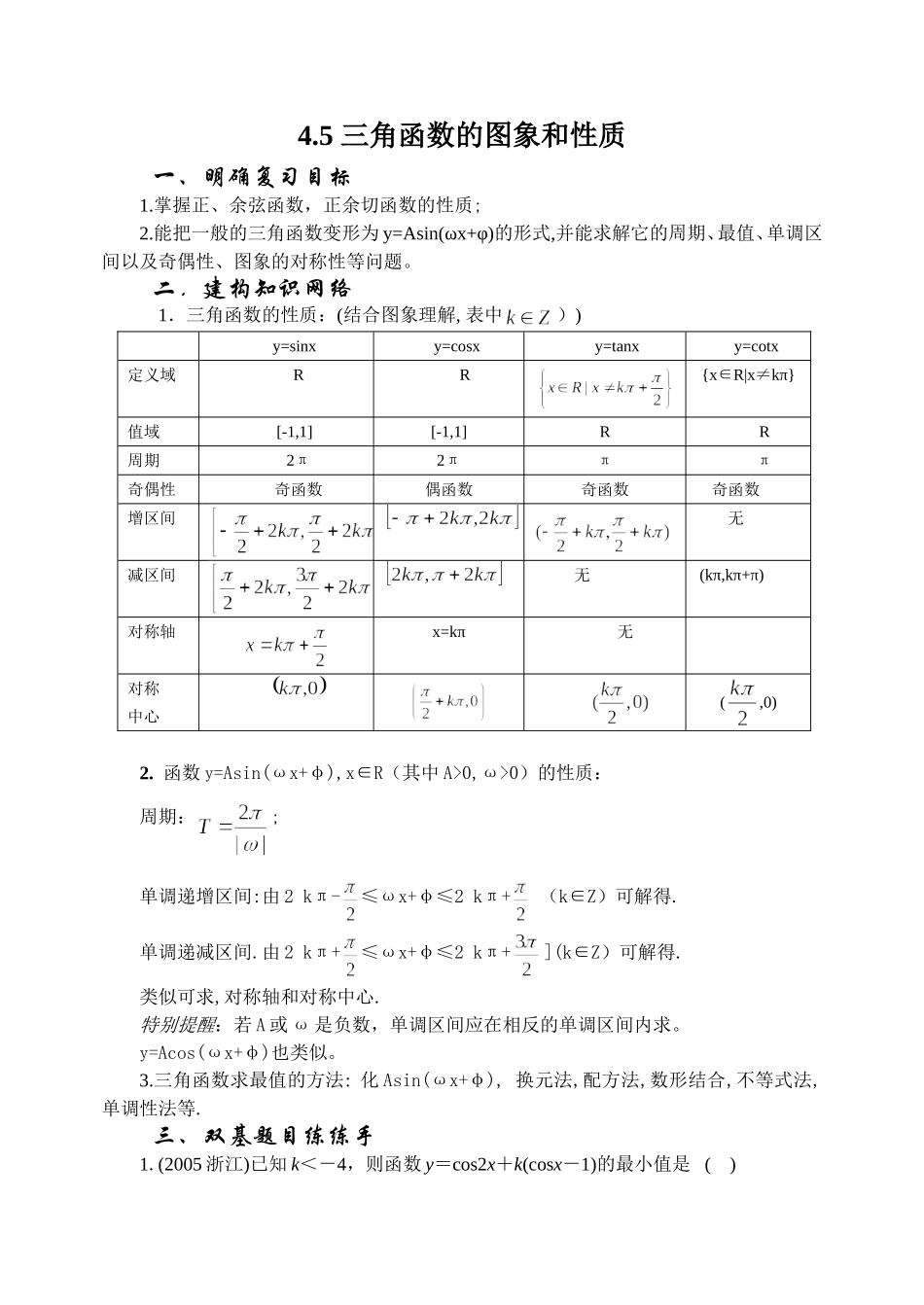
4.5三角函数的图象和性质一、明确复习目标1.掌握正、余弦函数,正余切函数的性质;2.能把一般的三角函数变形为y=Asin(ωx+φ)的形式,并能求解它的周期、最值、单调区间以及奇偶性、图象的对称性等问题。二.建构知识网络1.三角函数的性质:(结合图象理解,表中))y=sinxy=cosxy=tanxy=cotx定义域RR{x∈R|x≠kπ}值域[-1,1][-1,1]RR周期2π2πππ奇偶性奇函数偶函数奇函数奇函数增区间无减区间无(kπ,kπ+π)对称轴x=kπ无对称中心(,0)2.函数y=Asin(ωx+φ),x∈R(其中A>0,ω>0)的性质:周期:;单调递增区间:由2kπ-≤ωx+φ≤2kπ+(k∈Z)可解得.单调递减区间.由2kπ+≤ωx+φ≤2kπ+](k∈Z)可解得.类似可求,对称轴和对称中心.特别提醒:若A或ω是负数,单调区间应在相反的单调区间内求。y=Acos(ωx+φ)也类似。3.三角函数求最值的方法:化Asin(ωx+φ),换元法,配方法,数形结合,不等式法,单调性法等.三、双基题目练练手1.(2005浙江)已知k<-4,则函数y=cos2x+k(cosx-1)的最小值是()(A)1(B)-1(C)2k+1(D)-2k+12.(2006全国)函数的单调增区间为()ABCD3.(2005江西)设函数为()A.周期函数,最小正周期为B.周期函数,最小正周期为C.周期函数,数小正周期为D.非周期函数4.已知sinα+cosβ=1,则y=sin2α+cosβ的取值范围是__________.5.为了使y=sinωx(ω>0)在区间[0,1]上至少出现50次最大值,则ω的最小值是6.,的最小正周期是________.7.给出下列命题:①正切函数的图象的对称中心是唯一的;②y=|sinx|、y=|tanx|的周期分别为π、;③若x1>x2,则sinx1>sinx2;④若f(x)是R上的奇函数,它的最小正周期为T,则f(-)=0.其中正确命题的序号是____________.◆答案:1-3.ACA;4.y=sin2α-sinα+1=(sinα-)2+. cosβ=1-sinα.∴sinα∈[0,1]∴y∈[,1].(本题易错解为y=sin2α+1-sinα,sinα∈[-1,1],求y的取值范围.)5.49×T≤1,即×≤1,∴ω≥.答案思考:若条件改为在[x0,x0+1]上至少出现50次最大值呢?6.化为一个角的三角数周期是π;7.答案:④四、经典例题做一做【例1】(2003春北京)已知函数f(x)=,求f(x)的定义域,判断它的奇偶性,并求其值域.解:由cos2x≠0得2x≠kπ+,解得x≠+(k∈Z).所以f(x)的定义域为{x|x∈R且x≠+,k∈Z}.因为f(x)的定义域关于原点对称,且f(-x)===f(x),所以f(x)是偶函数.又当x≠+(k∈Z)时,f(x)===3cos2x-1=,所以f(x)的值域为{y|-1≤y<或<y≤2}.◆提炼方法:对复杂的函数式,要先化简为Asin(ωx+φ)+m,或Acos(ωx+φ)+m的形式,再讨论性质.【例2】锐角x、y满足sinycscx=cos(x+y)且x+y≠,求tany的最大值.和取最大值时角x的集合.解: sinycscx=cos(x+y),∴sinycscx=cosxcosy-sinxsiny,siny(sinx+cscx)=cosxcosy.∴tany====≤=,当且仅当tanx=时取等号.∴tany的最大值为.对应角x的集合为◆提炼方法:先由已知变换出tany与x的函数关系,再用不等式求最值;是三角、函数、不等式知识的综合应用。【例3】(2006辽宁)已知函数,.求:(I)函数的最大值及取得最大值的自变量的集合;(II)函数的单调增区间.(I)解法一:∴当,即时,取得最大值因此,取得最大值的自变量的集合是解法二:∴当,即时,取得最大值因此,取得最大值的自变量的集合是(II)解:由题意得,即因此,的单调增区间是【例4】是否存在实数a,使得函数在闭区间上的最大值是1?若存在,求出对应的a值?若不存在,试说明理由。解:当时,,令则,综上知,存在符合题意。◆思维点拨:化,闭区间上的二次函数的最值问题字母分类讨论思路。【研讨.欣赏】(2003江苏)已知函数上的偶函数,其图象关于点对称,且在区间上是单调函数.求的值。解:由是偶函数,得,即,所以,对任意x都成立,且,所以得,依题设,所以解得.由的图象关于点M对称,得,取得所以,…,….当k=0时,上是减函数;当k=1时,上是减函数;当时,上不是单调函数.所以,综合得.五.提炼总结以为师1.熟记三角函数的图象与各性质很重要.2.设参可以帮助理解,熟练了以后可以省却这个过程.3.要善于运用图象解题,数形结合,数形转化。同步练习4.5...