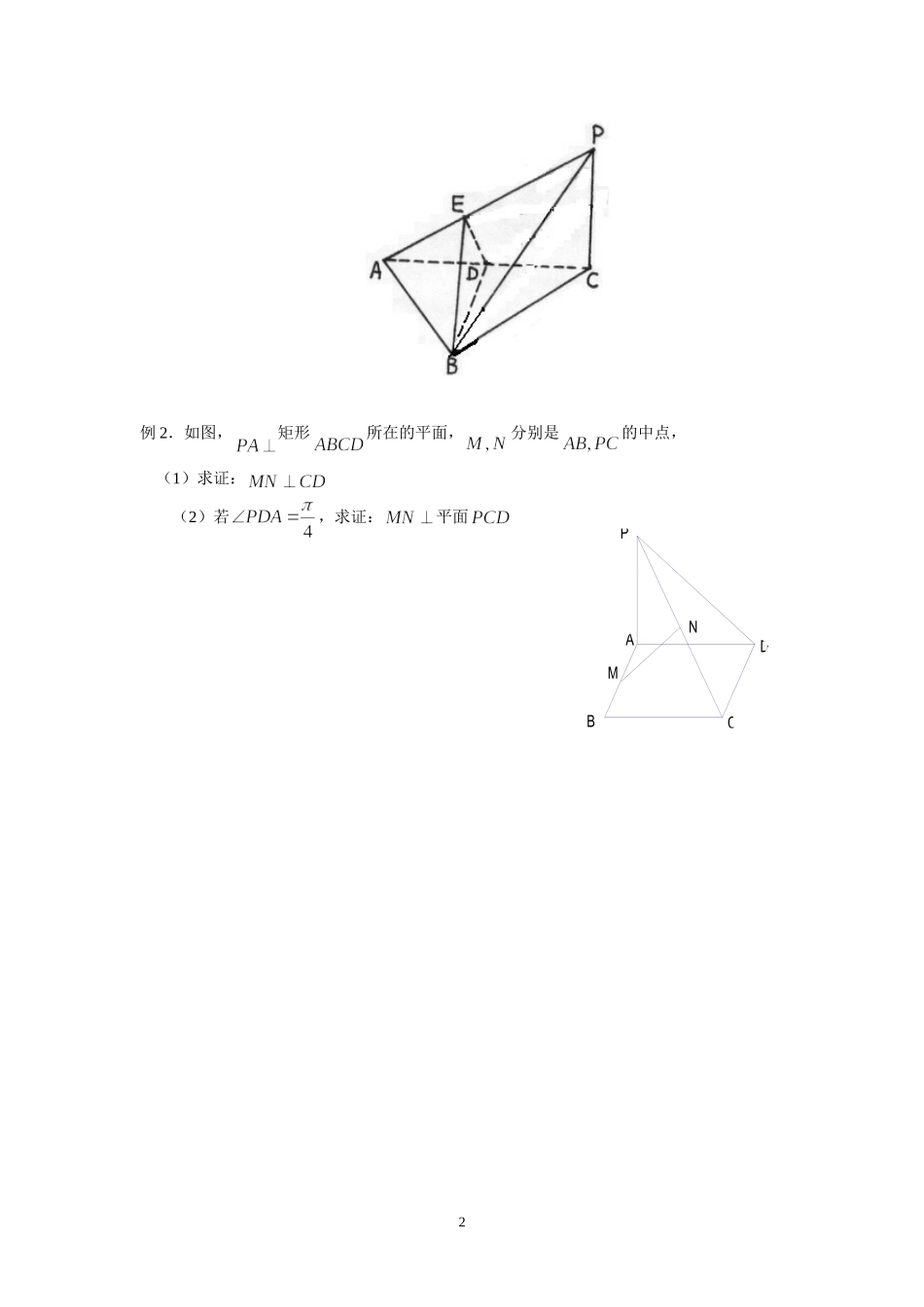
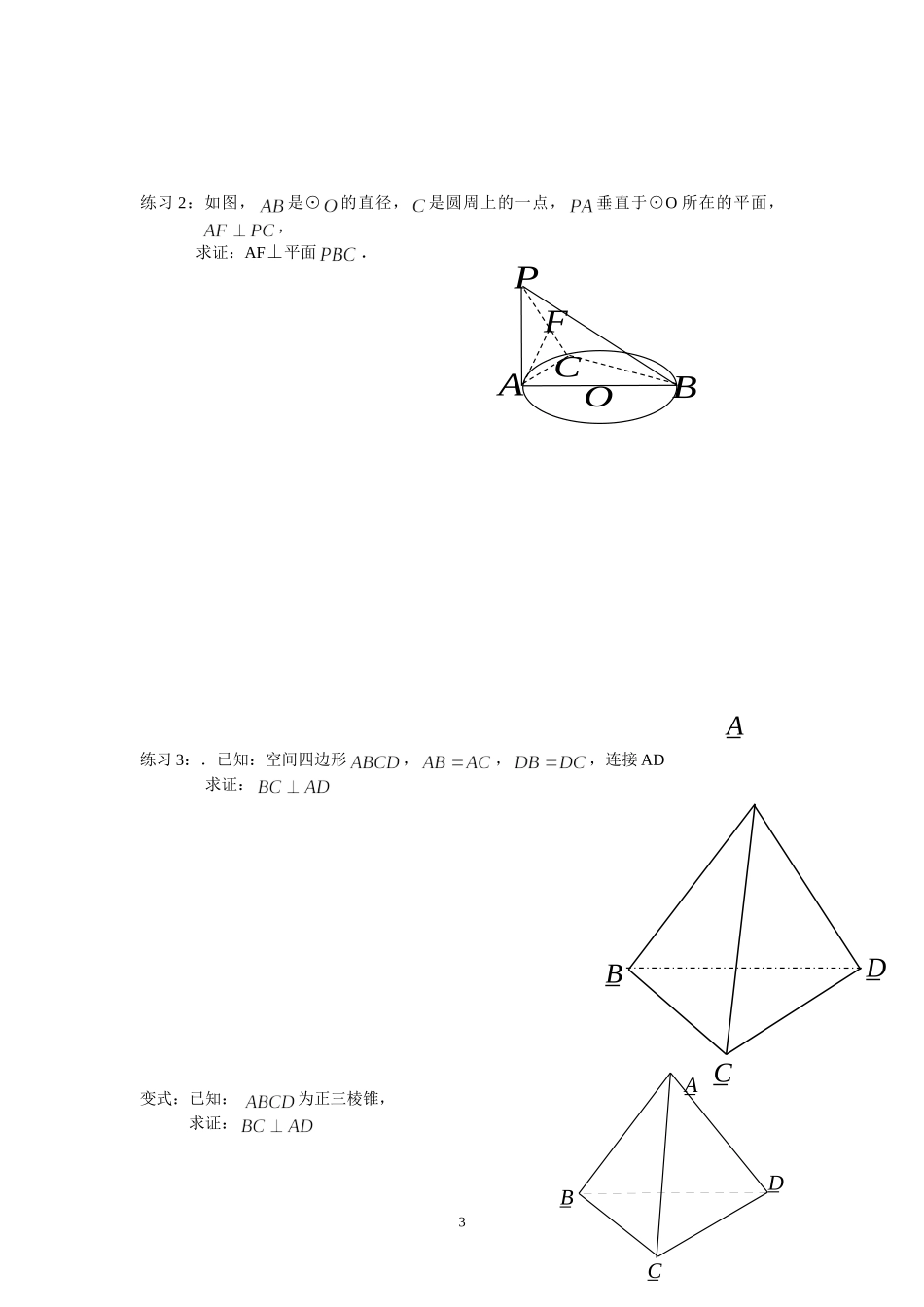
课题:直线与平面垂直教学目标:掌握直线与平面垂直的定义,直线与平面垂直的判定,提高学生的逻辑思维能力,培养学生由图形想象出位置的能力教学重点:直线和平面垂直的判定教学难点:直线和平面垂直的判定和应用教学过程一.知识概括1.直线与平面垂直的定义:如果一条直线l和一个平面α相交,并且和平面α内直线都垂直,我们就说直线l和平面α互相垂直奎屯王新敞新疆其中直线l叫做平面的垂线,平面α叫做直线l的垂面奎屯王新敞新疆交点叫做垂足奎屯王新敞新疆直线l与平面α垂直记作:lα⊥奎屯王新敞新疆2,直线与平面垂直的判定定理:如果一条直线和一个平面内的都垂直,那么这条直线垂直于这个平面奎屯王新敞新疆练习1:判断题(1)⊥与相交()(2)⊥,⊥⊥()(3)∥,∥,⊥⊥()(4)如果一条直线垂直于平面内的无数条直线,那么这条直线垂直这个平面()例1已知三棱锥P—ABC中,PC⊥底面ABC,AB=BC,D为AC的中点,DE⊥AP于E.求证:AP⊥平面BDE;1NMPDCBA例2.如图,矩形所在的平面,分别是的中点,(1)求证:(2)若,求证:平面2练习2:如图,是⊙的直径,是圆周上的一点,垂直于⊙O所在的平面,,求证:AF⊥平面.练习3:.已知:空间四边形,,,连接AD求证:变式:已知:为正三棱锥,求证:3BAOCFP_D_C_B_A_D_C_B_A二.小结线面垂直的常用判定方法:(1)定义法(2)线面垂直的判定定理(3)两条平行线中的一条垂直于一个平面,另一条也垂直于这个平面。(4)一条直线垂直于两个平行平面中的一个,也垂直于另一个平面。三.作业:复习资料第59—60页1—5题四.补充练习1.在空间四边形ABCD中,BC=AC,AD=BD,作BE⊥CD于E,作AH⊥BE于H,求证:AH⊥平面BCD2如图,ABCD为正方形,SA⊥面ABCD,过点A且垂直于SC的平面分别交SB、SC、SD于E、F、G.求证:AE⊥SB3.已知正方体,求证:⊥平面4.如图,几何体ABCDE中,△ABC是正三角形,EA和DC都垂直于平面ABC,且EA=AB=2a,DC=a,F、G分别为EB和AB的中点.(1)求证:FD∥平面ABC;(2)求证:AF⊥BD;45