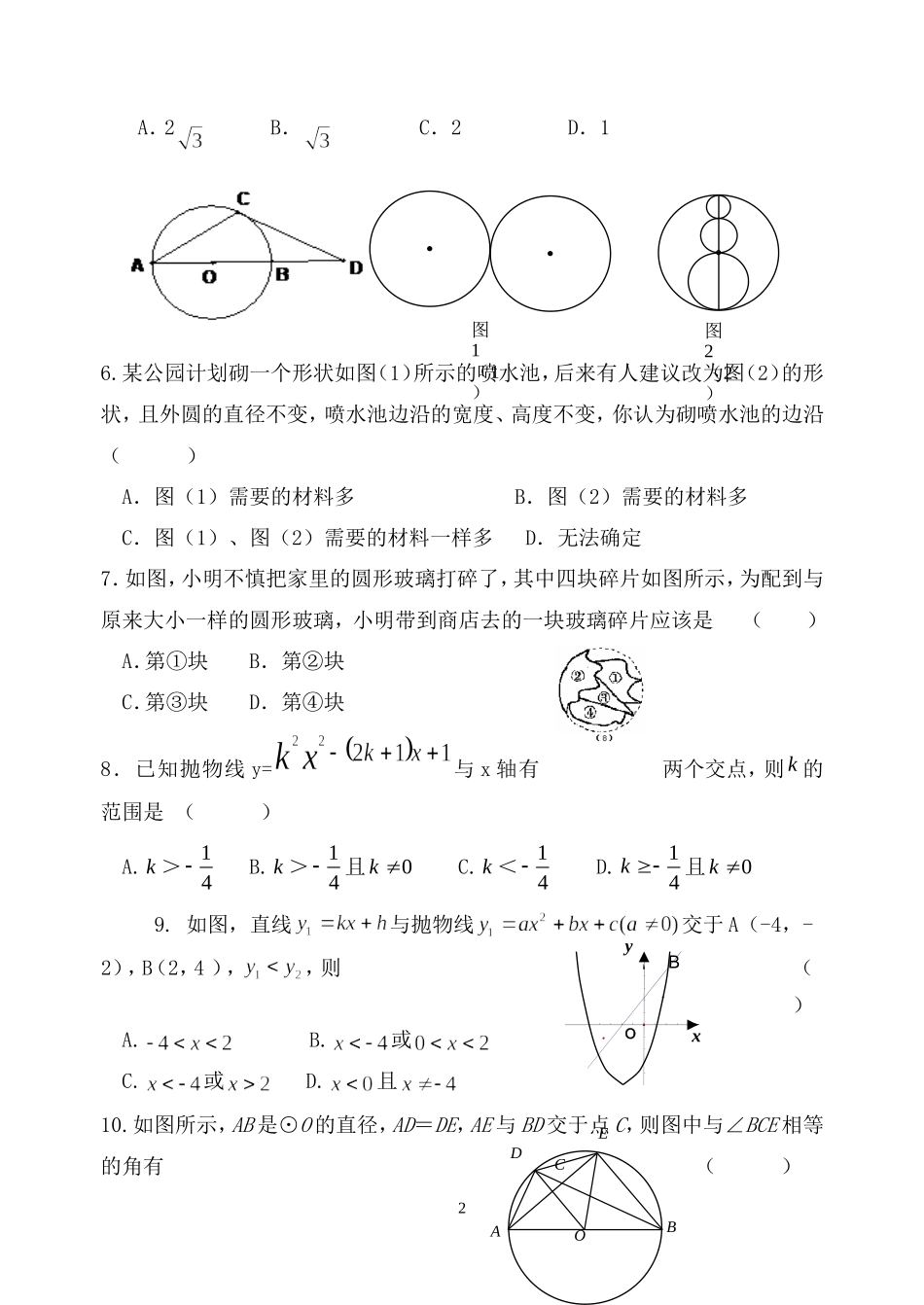
九年级数学月质量分析试卷一.选择题(每题3分,共30分)1.如果有意义,那么字母的取值范围是()A.B.C.D.2.下列图形中,既是轴对称图形,又是中心对称图形的有()A.1个B.2个C.3个D.4个3.把二次函数用配方法化成的形式()A.B.C.D.4.袋中放有一套(五枚)北京2008年奥运会吉祥物福娃纪念币,依次取出(不放回)两枚纪念币,恰好能够组成“欢迎”的概率是()A.251B.201C.101D.515.如图,若⊙O的直径AB与弦AC的夹角为30°,切线CD与AB的延长线交于点D,且⊙O的半径为1,则CD的长为()1贝贝晶晶欢欢迎迎妮妮A.2B.C.2D.16.某公园计划砌一个形状如图(1)所示的喷水池,后来有人建议改为图(2)的形状,且外圆的直径不变,喷水池边沿的宽度、高度不变,你认为砌喷水池的边沿()A.图(1)需要的材料多B.图(2)需要的材料多C.图(1)、图(2)需要的材料一样多D.无法确定7.如图,小明不慎把家里的圆形玻璃打碎了,其中四块碎片如图所示,为配到与原来大小一样的圆形玻璃,小明带到商店去的一块玻璃碎片应该是()A.第①块B.第②块C.第③块D.第④块8.已知抛物线y=与x轴有两个交点,则k的范围是()A.k>14B.k>14且0kC.k<14D.14k且0k9.如图,直线与抛物线交于A(-4,-2),B(2,4),,则()A.B.或C.或D.且10.如图所示,AB是⊙O的直径,AD=DE,AE与BD交于点C,则图中与∠BCE相等的角有()2xOBy图1(1)图2(2)BEDACOA.2个B.3个C.4个D.5个二.填空题(每题3分,共24分)11.=12.抛物线y=x2-4x-5与直线y=x+1的交点坐标为_________13.将一个底面半径为3cm,高为4cm圆锥形纸筒沿一条母线剪开,所得的侧面展开图的面积为_______________.14.将点A(0,4)绕着原点逆时针方向旋转45°角得到点B,则点B的坐标是.15.一种药品经过两次降价,药价从原来每盒50元降至现在32元,若平均每次降价的百分率为x,则方程可列为16.如图,从P点引⊙O的两切线PA、PA、PB,A、B为切点,已知⊙O的半径为2,∠P=60°,则图中阴影部分的面积为17.二次函数y=ax2+bx+c的图像如图所示,则点(b,),关于原点的对称点在第象限。18.半径为R的圆的内接正三角形与内接正六边形的面积之比为三.简答题19.计算(12分):①2313()|13|272②3xyO20.(6分)解一元二次方程:(配方法)21.(6分)先化简,再求值:,其中x=2-.22.(8分)如图,已知2抛物线的顶点坐标为(1,4),且过点(0,3),①求抛物线的解析式;②画出抛物线的图像③设抛物线与x轴交于A、E两点,交y轴于B点,顶点为D,求四边形AEDB的面积;23.(10分)已知关于x的一元二次方程有两个不相等的实根、,①求k的取值范围②是否存在实数k,使方程的两实数根互为相反数?若存在,求出k的值;若不存在,请说明理由。4DOCAB24.(10分)一个不透明的口袋里装有红、白、黄三种颜色的乒乓球(除颜色外其余都相同),其中有白球2个,黄球1个.若从中任意摸出一个球,这个球是白球的概率为0.5.①求口袋中红球的个数.②小明认为口袋中共有三种颜色的球,所以从袋中任意摸出一球,放回,再任意摸出第二个球,则两次都摸到红球的概率是,你认为对吗?若不对,请你用列表或画树状图的方法说明理由.25.(10分)如图,在以O为圆心的两个同心圆中,AB经过圆心O,且与小圆相交于点A、与大圆相交于点B。小圆的切线AC与大圆相交于点D,且CO平分∠ACB。①试判断BC所在直线与小圆的位置关系,并说明理由;②试判断线段AC、AD、BC之间的数量关系,并说明理由;③若AB=8㎝,BC=10㎝,求大圆与小圆围成的圆环的面积。(结果保留π)526.(10分)跳绳时,绳甩到最高处时的形状是抛物线.正在甩绳的甲、乙两名同学拿绳的手间距AB为6米,到地面的距离AO和BD均为0.9米,身高为1.4米的小丽站在距点O的水平距离为1米的点F处,绳子甩到最高处时刚好通过她的头顶点E.以点O为原点建立如图所示的平面直角坐标系,设此抛物线的解析式为y=ax2+bx+0.9.①求该抛物线的解析式;②如果小华站在OD之间,且离点O的距离为3米,当绳子甩到最高处时刚好通过他的头顶,请你算出小华的身高;③如果身高为1.4米的小丽站在OD之间,且离点O的距离...