高三数学一轮复习 第4单元 4.3 平面向量的数量积及平面向量应用随堂训练 理 新人教B版VIP免费

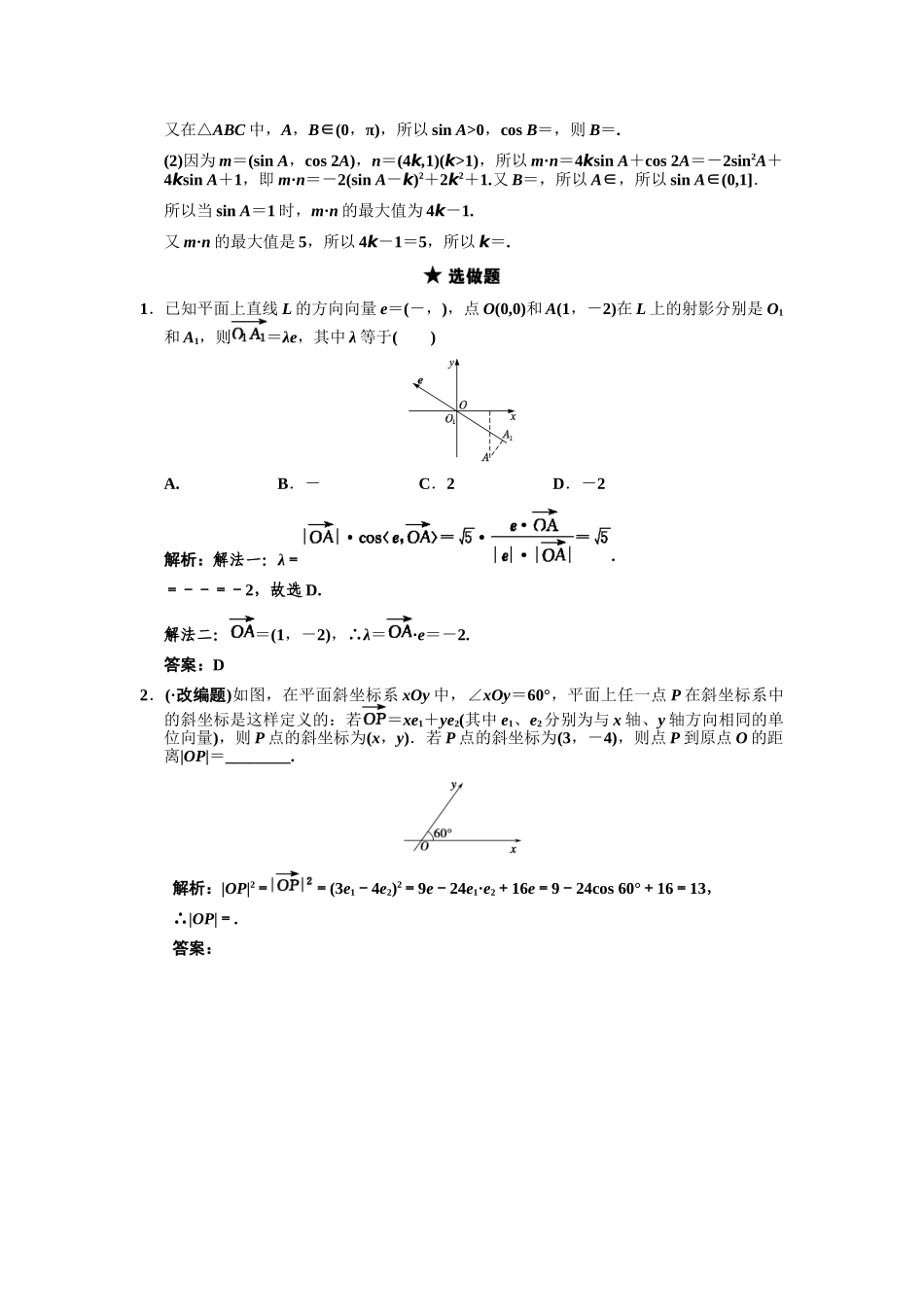
4.3平面向量的数量积及平面向量应用举例一、选择题1．(·辽宁)平面向量a与b的夹角为60°，a＝(2,0)，|b|＝1，则|a＋2b|＝()A.B．2C．4D．12解析：因为a＝(2,0)，|b|＝1，所以|a|＝2，a·b＝2×1×cos60°＝1，故|a＋2b|＝＝2.答案：B2．已知|a|＝2，|b|＝4，向量a与b的夹角为60°，当(a＋3b)⊥(ka－b)时，实数k的值是()A.B.C.D.解析：依题意得a·b＝|a|·|b|·cos60°＝2×4×＝4，因为(a＋3b)⊥(ka－b)，所以(a＋3b)·(ka－b)＝0，得ka2＋(3k－1)a·b－3b2＝0，即k＋3k－1－12＝0，解得k＝.答案：C3．(·浙江)已知向量a＝(1,2)，b＝(2，－3)．若向量c满足(c＋a)∥b，c⊥(a＋b)，则c＝()A.B.C.D.解析：不妨设c＝(m，n)，则a＋c＝(1＋m,2＋n)，a＋b＝(3，－1)，对于(c＋a)∥b，则有－3(1＋m)＝2(2＋n)；又c⊥(a＋b)，则有3m－n＝0，则有m＝－，n＝－.答案：D4．(·广东)一质点受到平面上的三个力F1、F2、F3(单位：牛顿)的作用而处于平衡状态，已知F1、F2成60°角，且F1、F2的大小分别为2和4，则F3的大小为()A．2B．2C．2D．6解析：由已知条件F1＋F2＋F3＝0，则F3＝－F1－F2因此F32＝(F1＋F2)2＝F12＋F22＋2F1·F2＝22＋42＋2×2×4cos60°＝28，所以|F3|＝2.答案：A二、填空题5．(·北京东城一模)已知两个向量a＝(1,2)，b＝(x,1)，若(a＋2b)∥(2a－2b)，则x的值为________．解析：a＋2b＝(1＋2x,4),2a－2b＝(2－2x,2)，∵(a＋2b)∥(2a－2b)，∴(1＋2x)×2－(2－2x)×4＝0，∴x＝.答案：6．向量a，b，c，满足a＋b＋c＝0，(a－b)⊥c，a⊥b，若|a|＝1，则|a|2＋|b|2＋|c|2的值是________．解析：解法一：由已知a·c－b·c＝0，a·b＝0，|a|＝1，又a＋b＋c＝0，∴a·(a＋b＋c)＝0,即a2＋a·c＝0，则a·c＝－1，由a＋b＋c＝0，∴(a＋b＋c)2＝0，即a2＋b2＋c2＋2a·b＋2b·c＋2c·a＝0，∴a2＋b2＋c2＝－4c·a＝4.解法二：由已知条件向量a、b、c的关系如图所示．可观察出|a|＝|b|＝1，|c|＝，∴|a|2＋|b|2＋|c|2＝4.答案：47.(·天津)若等边的边长为2，平面内一点Ｍ满足.解析:所以答案:－2三、解答题8．已知平面向量a＝(1，x)，b＝(2x＋3，－x)(x∈R)．(1)若a⊥b，求x的值；(2)若a∥b，求|a－b|.解答：(1)若a⊥b，则a·b＝(1，x)·(2x＋3，－x)＝1×(2x＋3)＋x(－x)＝0.整理得：x2－2x－3＝0，解得：x＝－1或x＝3.(2)若a∥b，则有1×(－x)－x(2x＋3)＝0，即x(2x＋4)＝0.解得：x＝0或x＝－2.当x＝0时，a＝(1,0)，b＝(3,0)，∴|a－b|＝|(1,0)－(3,0)|＝|(－2,0)|＝＝2；当x＝－2时，a＝(1，－2)，b＝(－1,2)，∴|a－b|＝|(1，－2)－(－1,2)|＝|(2，－4)|＝＝2.9．(·江苏)设向量a＝(4cosα，sinα)，b＝(sinβ，4cosβ)，c＝(cosβ，－4sinβ)．(1)若a与b－2c垂直，求tan(α＋β)的值；(2)求|b＋c|的最大值；(3)若tanαtanβ＝16，求证：a∥b.解答：(1)因为a与b－2c垂直，所以a·(b－2c)＝4cosαsinβ－8cosαcosβ＋4sinαcosβ＋8sinαsinβ＝4sin(α＋β)－8cos(α＋β)＝0，因此tan(α＋β)＝2.(2)由b＋c＝(sinβ＋cosβ，4cosβ－4sinβ)，得|b＋c|＝＝≤4.又当β＝－时，等号成立，所以|b＋c|的最大值为4.(3)由tanαtanβ＝16得＝，所以a∥b.10．(·江苏苏北四市调研)在△ABC中，角A，B，C的对边分别为a，b，c，且满足(2a－c)cosB＝bcosC.(1)求角B的大小；(2)设m＝(sinA，cos2A)，n＝(4k,1)(k>1)，且m·n的最大值是5，求k的值．解答：(1)因为(2a－c)cosB＝bcosC，所以在△ABC中，由正弦定理得，(2sinA－sinC)cosB＝sinBcosC，所以2sinAcosB＝sinBcosC＋cosBsinC，即2sinAcosB＝sinA.又在△ABC中，A，B∈(0，π)，所以sinA>0，cosB＝，则B＝.(2)因为m＝(sinA，cos2A)，n＝(4k,1)(k>1)，所以m·n＝4ksinA＋cos2A＝－2sin2A＋4ksinA＋1，即m·n＝－2(sinA－k)2＋2k2＋1.又B＝，所以A∈，所以sinA∈(0,1]．所以当sinA＝1时，m·n的最大值为4k－1.又m·n的最大值是5，所以4k－1＝5，所以k＝.1．已知平面上直线L的方向向量e＝(－，)，点O(0,0)和A(1，－2)在L上的射影分别是O1和A1，则＝λe，其中λ等于()A.B．－C．2D．－2解析：解法一：λ＝·＝－－＝－2，故选D.解法二：＝(1，－2)，∴λ＝·e＝－2.答案：D2．(·改编题)如图，在平面斜坐标系xOy中，∠xOy＝60°，平面上任一点P在斜坐标系中的斜坐标是这样定义的：若＝xe1＋ye2(其中e1、e2分别为与x轴、y轴方向相同的单位向量)，则P点的斜坐标为(x，y)．若P点的斜坐标为(3，－4)，则点P到原点O的距离|OP|＝________.解析：|OP|2＝＝(3e1－4e2)2＝9e－24e1·e2＋16e＝9－24cos60°＋16＝13，∴|OP|＝.答案：