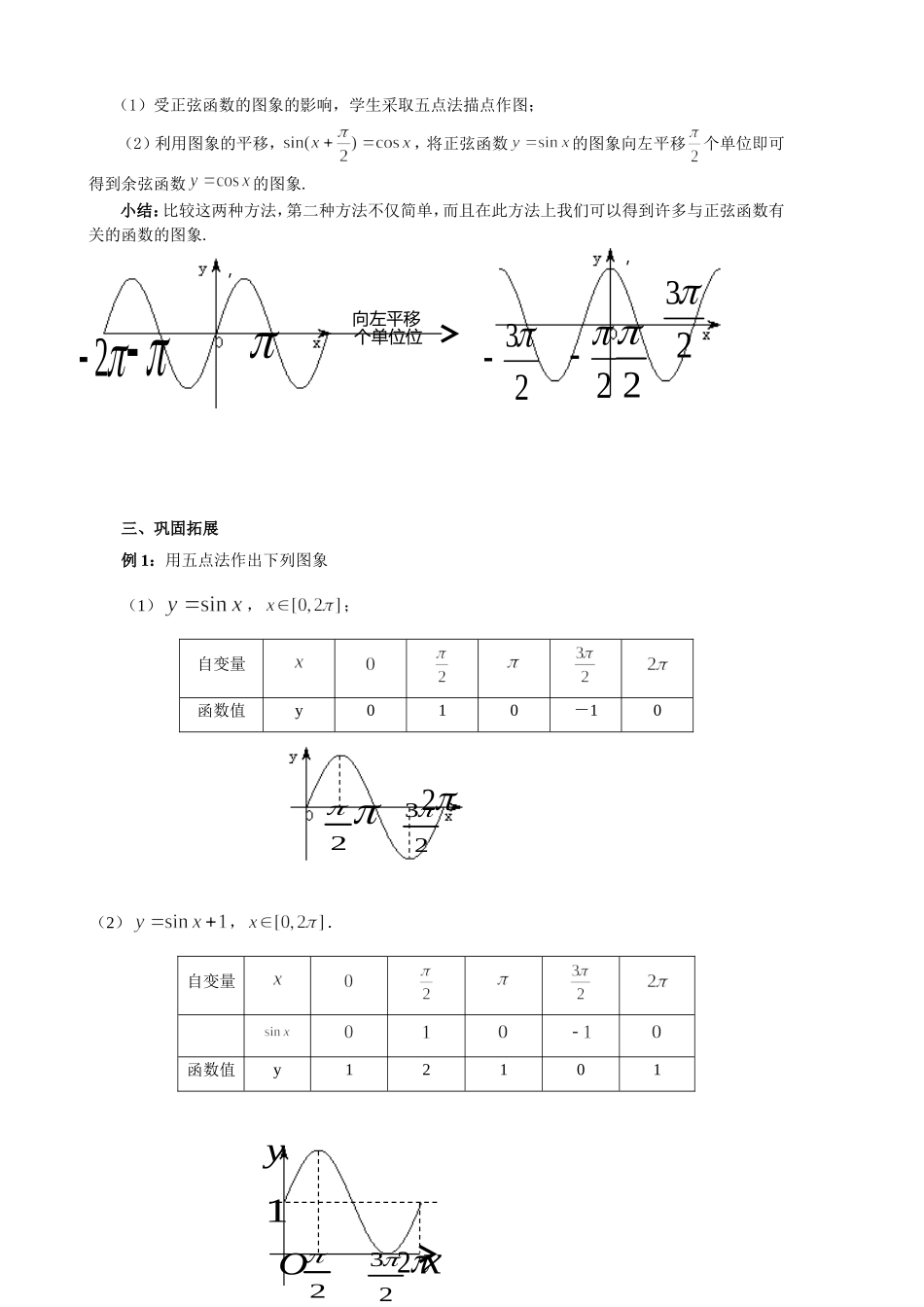
第一章三角函数1.4三角函数的图象与性质1.4.1正弦函数、余弦函数的图象[教学目标]一、知识与能力:1.会用五点法画正弦、余弦函数的图象;2.记住正弦、余弦函数的特征;3.弄清正弦、余弦函数的图象之间的关系.二、过程与方法:利用单位圆中的正弦线作正弦函数图象,利用诱导公式,经过平移,得到余弦函数图象.三、情感、态度与价值观:体会正、余函数的图象并能利用其观察和解释一些自然现象.[教学重点]几何法作正弦曲线.[教学难点]五点作图法做正、余弦函数的图象.[教学方法]创设情境—主体探究—合作交流—应用提高.[教学过程]一、创设问题情境,激发学生兴趣,引出本节内容1.复习:学生口述函数的定义.2.引入:教师活动:结合我们刚学过的三角比,就以正弦(或余弦)为例,对每一个给定的角和正弦值(或)之间是否也存在一种函数关系?若存在,请对这种函数关系下一个定义,若不存在请说明理由.3.讨论:对自变量的取值类型和范围进行讨论,并给出相应的正弦函数和余弦函数的符号.以往我们在研究函数时,先探究函数所具备的性质,再作出函数的图象,今天我们先探究正弦函数和余弦函数的图象,再得出函数的性质.二、传授新识1.三角函数的定义对每一个实数都对应惟一确定的角度,这个确定的角度又对应惟一确定的正弦值(或余弦值),即每一个实数都有唯一确定的值(或)与之对应,按这一对应法则建立的关系是一个函数关系,表示为(或),称为正弦函数(或余弦函数).正余弦函数的定义域为全体实数.2、利用单位圆中正弦线作正弦函数图象(1)教师帮助学生回忆单位圆中的正弦线和余弦线设点P为单位圆上任意一点,的一个角为,Q为点P在x轴上的投影,则有向线段QP的长是对应的正弦线,有向线段OQ的长是对应的余弦线.让学生结合三角比的定义及对不同象限的角的正弦值和余弦值加以验证.(2)演示单位圆的课件,让学生体验、加深理解.(3)小组讨论在单位圆中正弦线和余弦线在随角变化而变化的规律,并归纳总结.(4)设计画正弦函数的图象的方案.利用作出,,……及,……的正弦函数的图象.(5)展示学生的作品,演示正弦函数的课件.(6)归纳作正弦函数时的心得:1、先确定五点(0,0),,,,;2、再用光滑曲线连接,注意曲线弯曲特征;3、通过图象平移得到其他范围上的图象.具体作法:(几何作法)(1)在直角坐标系的轴上任取一点,以为圆心作单位圆,从⊙与轴的交点起,把⊙分成等份,过⊙上各点作轴的垂线,可得对应于等角的正弦线;(2)把轴上这一段分成等份,把角的正弦线向右平行移动,使正弦线的起点与轴上的点重合;(3)用光滑曲线把这些正弦线的终点连结起来,就得到正弦函数,的图象.(4)因为终边相同的角的函数值相同,所以,函数,()且的图象与函数,的图象的形状完全相同,只是位置不同,于是只要将函数,的图象向左、右平移,就可得到函数,的图象.3.余弦函数的图象探究:我们已经有了正弦函数的图象,那我们如何得到余弦函数的图象?(让学生小组共同探究)学生活动:得到的可能的方法:0xPyxQ,2,232232(1)受正弦函数的图象的影响,学生采取五点法描点作图;(2)利用图象的平移,,将正弦函数的图象向左平移个单位即可得到余弦函数的图象.小结:比较这两种方法,第二种方法不仅简单,而且在此方法上我们可以得到许多与正弦函数有关的函数的图象.三、巩固拓展例1:用五点法作出下列图象(1),;自变量函数值y010-10(2),.自变量函数值y12101向左平移个单位位yxO321223222四、小结作业1、小结:(1)正弦函数和余弦函数的定义(2)单位圆中的正弦线和余弦线(3)正弦函数和余弦函数的图象及其作法,简单的图象特征(4)函数图象平移中的方法及注意点2、作业课本P34练习1、2、31.4.2正弦函数、余弦函数的性质(1)——周期性[教学目标]一、知识与能力:1.理解周期函数、最小正周期的定义;2.会求正、余弦函数的最小正周期.二、过程与方法:利用单位圆探索三角函数的性质,渗透数形结合的数学思想三、情感、态度与价值观:体会函数的周期性并能利用其观察和解释一些自然现象.[教学重点]函数的周期性、最小正周期...