共线向量与共面向量VIP免费

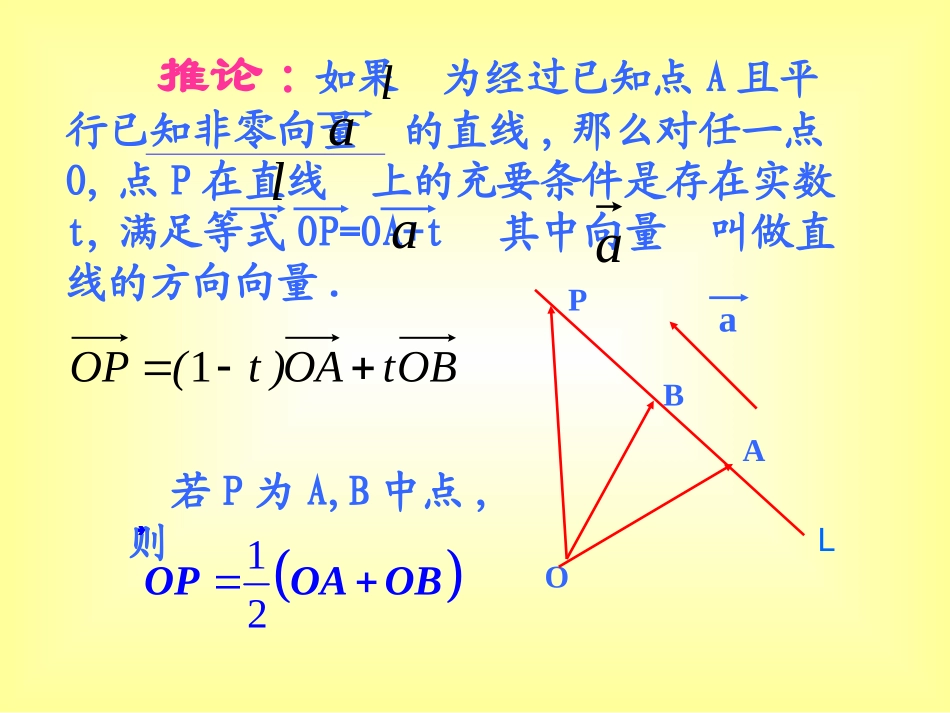
共线向量与共面向量一、共线向量:零向量与任意向量共线.1.共线向量:如果表示空间向量的有向线段所在直线互相平行或重合,则这些向量叫做共线向量(或平行向量),记作ba//2.共线向量定理:对空间任意两个向量的充要条件是存在实数使baobba//),(,ba推论:如果为经过已知点A且平行已知非零向量的直线,那么对任一点O,点P在直线上的充要条件是存在实数t,满足等式OP=OA+t其中向量叫做直线的方向向量.llaaB若P为A,B中点,则12�OPOAOBOAPaLaOBtOA)t(OP13.共面向量定理:如果两个向量不共线,则向量与向量共面的充要条件是存在实数对使3.共面向量定理:如果两个向量不共线,则向量与向量共面的充要条件是存在实数对使,abyx,�Pxayb�p,abMabABAPp�推论:空间一点P位于平面MAB内的充要条件是存在有序实数对x,y使或对空间任一点O,有�MPxMAyMB�OPOMxMAyMBMabABAPp�O例3对空间任意一点O和不共线的三点A、B、C，试问满足向量关系式（其中）的四点P、A、B、C是否共面？�OPxOAyOBzOC1xyz例4已知A、B、M三点不共线，对于平面ABM外的任一点O，确定在下列各条件下，点P是否与A、B、M一定共面？(1)3OBOMOPOA�＋－(2)4OPOAOBOM�D'A'B'C'DABCO例5,如图，已知平行四边形ABCD，从平面AC外一点O引向量OA’=kOA,OB’=kOB,OC’=kOC,OD’=kOD,求证：⑴四点A’、B’、C’、D’共面；⑵平面A’C’//平面AC。1.对于空间中的三个向量它们一定是：A.共面向量B.共线向量C.不共面向量D.既不共线又不共面向量2MAMBMAMB�、、－2.已知点M在平面ABC内，并且对空间任意一点O，,则x的值为：OMxOAOBOC�11＋＋331.1.0.3.3ABCD三、课堂小结：1.共线向量的概念。2.共线向量定理。3.共面向量的概念。4.共面向量定理。