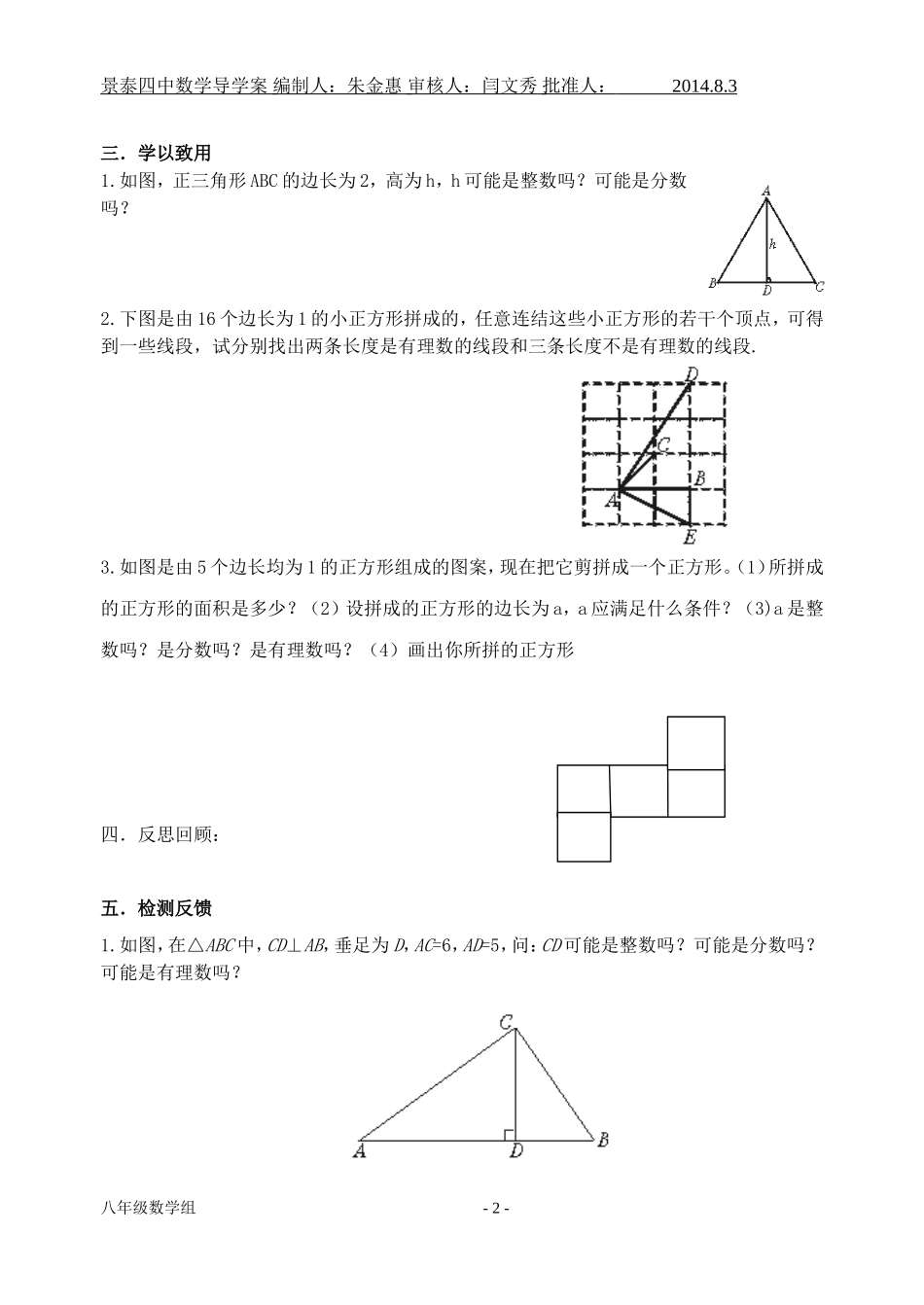
景泰四中数学导学案编制人:朱金惠审核人:闫文秀批准人:2014.8.3编号:8s2012.1.1认识无理数(1)班级组号姓名学习目标:1.通过拼图活动,让学生感受无理数产生的实际背景和引入的必要性.2.能判断给出的数是否为有理数;并能说出理由.学习重点:会判断一个数是否为有理数.学习难点:会判断一个数是否为有理数.预习指导:1.先精读教材P21,用红色笔勾画知识点。再针对学案二次阅读教材,完成教材助读设置的问题,依据发现的问题,查阅资料,解决有关问题。2.找出自己的疑惑和需要讨论的问题,记录在预习学案上,准备课上讨论质疑。3.预习目标:独立,限时完成预习自测,并把自己的疑惑写出来.学习环节:一.自学导航1.以下各数:-1,,3.14,-π,3.,0,2,,,-0.2020020002……(相邻两个2之间0的个数逐次加)是有理数的是_____________,2.(1)将两个边长为1的正方形,动手剪一剪,拼一拼,设法得到一个大的正方形,有几种拼法,画出图形?.(2).假设拼成大正方形的边长为a,则a应满足什么条件呢?a是整数吗?a是分数吗?为什么?二.合作探究1.在下图中,以直角三角形的斜边为边的正方形的面积是多少?(2)设该正方形的边长为b,则b应满足什么条件?(3)b是有理数吗?八年级数学组-1-景泰四中数学导学案编制人:朱金惠审核人:闫文秀批准人:2014.8.3三.学以致用1.如图,正三角形ABC的边长为2,高为h,h可能是整数吗?可能是分数吗?2.下图是由16个边长为1的小正方形拼成的,任意连结这些小正方形的若干个顶点,可得到一些线段,试分别找出两条长度是有理数的线段和三条长度不是有理数的线段.3.如图是由5个边长均为1的正方形组成的图案,现在把它剪拼成一个正方形。(1)所拼成的正方形的面积是多少?(2)设拼成的正方形的边长为a,a应满足什么条件?(3)a是整数吗?是分数吗?是有理数吗?(4)画出你所拼的正方形四.反思回顾:五.检测反馈1.如图,在△ABC中,CD⊥AB,垂足为D,AC=6,AD=5,问:CD可能是整数吗?可能是分数吗?可能是有理数吗?八年级数学组-2-景泰四中数学导学案编制人:朱金惠审核人:闫文秀批准人:2014.8.3编号:8s2022.1.2认识无理数(2)班级组号姓名学习目标:1.借助计算器探索无理数是无限不循环小数,并从中体会无限逼近的思想.2.会判断一个数是有理数还是无理数.学习重点:1.无理数概念的探索过程.学习难点:1.无理数概念的建立及估算.预习指导:1.先精读教材P22,用红色笔勾画知识点。再针对学案二次阅读教材,完成教材助读设置的问题,依据发现的问题,查阅资料,解决有关问题。2.找出自己的疑惑和需要讨论的问题,记录在预习学案上,准备课上讨论质疑。学习环节:一.自学导航1.观察P34表格,估算面积为2的正方形的边长a为多少?边长a面积S1<a<21<S<41.4<a<1.5<S<1.41<a<1.421.9881<S<2.01641.414<a<1.4151.999396<S<2.0022251.4142<a<1.41431.99996164<S<2.000244492.边长a的整数部分是,十分位是,百分位是它是有限小数吗?3.把下列各数表示成小数.3,,并看它们是有限小数还是无限小数,是循环小数还是不循环小数?4.设面积为5π的圆的半径为a.(1)a是有理数吗?说说你的理由.(2)估计a的值(精确到十分位,并利用计算器验证你的估计).二.合作探究1.无理数的定义:无限不循环小数叫无理数(irrationalnumber).2.有理数与无理数的主要区别(1)无理数是无限不循环小数,有理数是有限小数或无限循环小数.(2)任何一个有理数都可以化为分数的形式,而无理数则不能.3.如图,四边形ABCD是5x5网格中的格点正方形,网格中每个小正方形的边长均为1.(1)求正方形ABCD的面积(2)正方形ABCD的边长是有理数还是无理数?它在哪两个整数之间?AA八年级数学组-3-景泰四中数学导学案编制人:朱金惠审核人:闫文秀批准人:2014.8.3BDC4.判断题(1)有理数与无理数的差都是有理数.(2)无限小数都是无理数.(3)无理数都是无限小数.(4)两个无理数的和不一定是无理数.三.学以致用1.下列数中是无理数的是()A.0.12B.C.0D.2.下列说法中正确的是()A.不循环小数是无理数B.分数不是有理数C.有理数都是有限小数D.3.1415926是有理数3.下列语句正确的是()A.3.78788...