人教新版数学七下522平行线的判定（第1课时）课件VIP免费

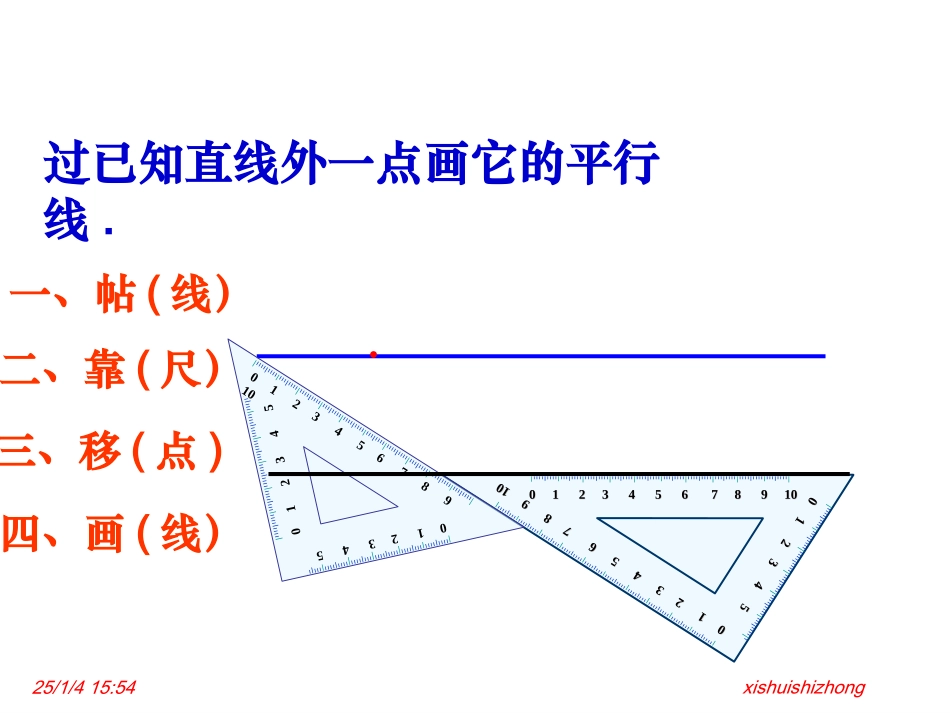
5.2.2平行线的判定(1)25/1/415:54xishuishizhong（1）平面内两条直线的位置关系有几种？（2）怎样过已知直线外一点画已知直线的平行线？相交与平行25/1/415:54xishuishizhong一、帖(线）二、靠(尺）三、移(点)四、画(线）012345012345012345678910012345678910012345678910012345678910012345678910012345012345●过已知直线外一点画它的平行线.25/1/415:54xishuishizhong观察与发现:1l2lAB在画图过程中,什么角始终保持相等?由此你能发现判定两直线平行的方法吗?25/1/415:54xishuishizhong一般地,判断两直线平行有下面的方法:判定方法1两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.简单说成：同位角相等同位角相等,,两直线平行两直线平行.25/1/415:54xishuishizhong如图：（如图：（11）由）由1=1=22，，可推出可推出a//ba//b吗？为什么？吗？为什么？说一说说一说答：可以推出答：可以推出a//b.a//b.根据同位角相等，两直线平行根据同位角相等，两直线平行答：可以推出答：可以推出a//b.a//b.根据同位角相等，两直线平行根据同位角相等，两直线平行12abc25/1/415:54xishuishizhong12abc ∠1=2∠（已知）∴ab∥（同位角相等，两直线平行）书写格式：25/1/415:54xishuishizhong4123ABCEFD5HG如果,能判定哪两条直线平行?∠1=2∠∠2=5∠∠3=4∠想一想25/1/415:54xishuishizhong两条直线被第三条直线所截，同时得到同位角、内错角和同旁内角，由同位角相等可以判定两直线平行，那么，能否利用内错角，或同旁内角来判定两直线平行呢？思考：25/1/415:54xishuishizhong（（22）由）由3=3=22，可推出，可推出a//ba//b吗？吗？如何推出？写出你的推理过程如何推出？写出你的推理过程25/1/415:54xishuishizhong•解：解：1=1=3(3(已知）已知）•3=3=22（对顶角相等）（对顶角相等）•1=1=22•a//b(a//b(同位角相等，两直线平行）同位角相等，两直线平行）21cba3说一说说一说数学转化思想判定方法2两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行简单说成：内错角相等,两直线平行一般地,判断两直线平行有下面的方法:25/1/415:54xishuishizhong如图，∠1=2∠，且∠1=∠3，AB和CD平行吗？ABCD123想一想25/1/415:54xishuishizhong（3）如果1+1+2=1802=18000能判定能判定a//ba//b吗吗??c解:能,因为1+1+2=1802=1801+1+3=1803=180所以所以2=2=33所以所以a//ba//b2ba13说一说说一说数学转化思想25/1/415:54xishuishizhong判定方法3两条直线被第三条直线所截,如果同旁内角互补同旁内角互补,那么这两条直线平行简单说成：同旁内角互补同旁内角互补,两直线平行一般地,判断两直线平行有下面的方法:25/1/415:54xishuishizhong如图：如图：B=B=D=45°D=45°，，C=135°C=135°，，问图中有哪些直线平行？问图中有哪些直线平行？答：答：AB//CDAB//CD，，AD//BCAD//BC B=45°B=45°（已知）（已知）C=135°C=135°（已知）（已知）B+B+C=180°C=180°AB//CDAB//CD（同旁内角互补，两直线平行）（同旁内角互补，两直线平行）同理：同理：AD//BCAD//BCDCBA想一想25/1/415:54xishuishizhong同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行；归纳归纳25/1/415:54xishuishizhong判定两条直线平行的方法文字叙述符号语言图形相等两直线平行 (已知)∴ab∥相等两直线平行 (已知)∴ab∥互补，两直线平行 ∴ab∥同位角内错角同旁内角∠1=2∠∠3=2∠∠2+4=180°∠abc123425/1/415:54xishuishizhong能力挑战（（AA∠）∠）22∠＝∠＝33（（BB∠）∠）11＝＝∠∠44（（CC∠）∠）11∠＝∠＝22（（DD∠）∠）11＝＝∠∠33DD11、如图、如图,,不能判定的是（）不能判定的是（）12//ll13241l2l25/1/415:54xishuishizhong能力挑战22、如图、如图,,∠∠11＝∠＝∠2,2,则下列结论正确的是（则下列结论正确的是（））ABCDEF12（（AA））AD//BCAD//BC（（BB））AB//CDAB//CD（（CC））AD//EFAD//EF（（DD））EF//BCEF//BCCC25/1/415:5...