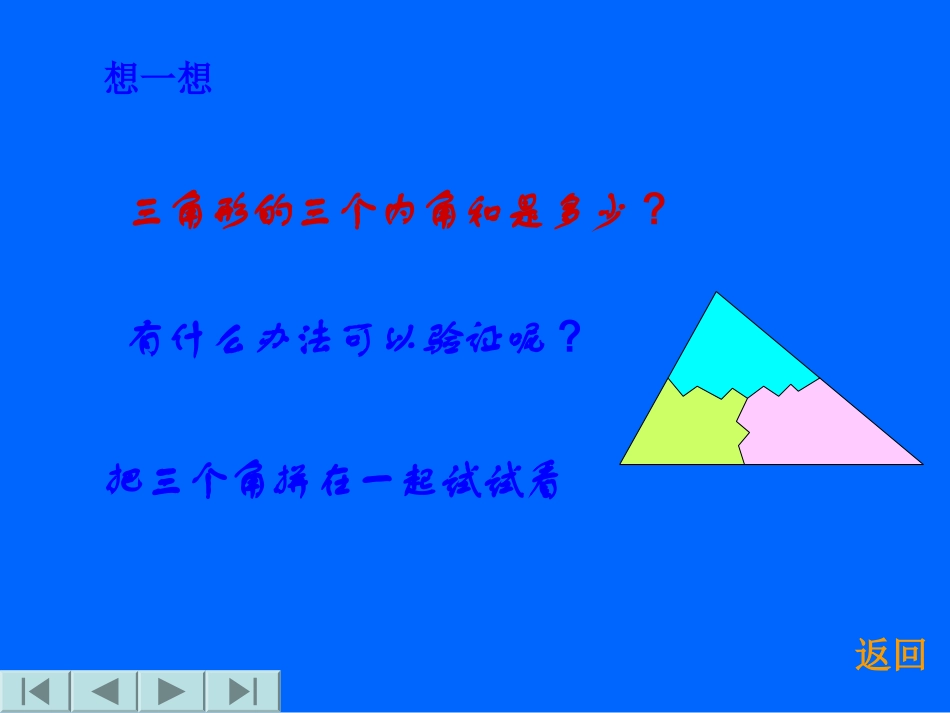
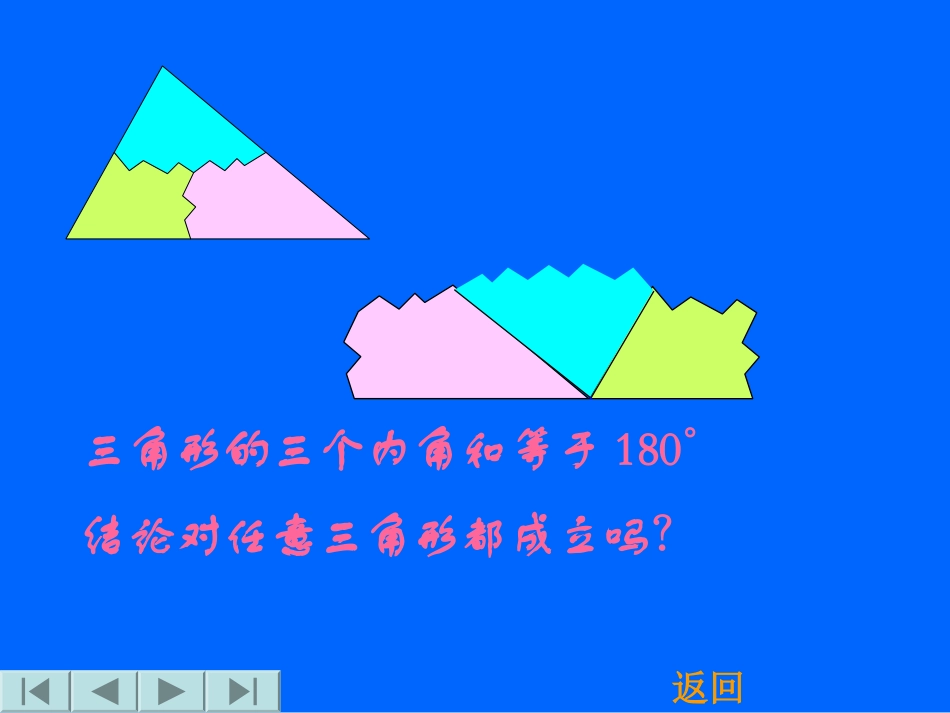
三角形的内角和市二中张书锋想一想三角形的三个内角和是多少?把三个角拼在一起试试看有什么办法可以验证呢?返回三角形的三个内角和等于180°结论对任意三角形都成立吗?返回AD过C作CEBA∥,)E1。于是∠A=1∠(两直线平行,内错角相等)∠B=2∠又∵∠1+2+ACB=180°∠∠(平角的定义)∴∠A+B+ACB=180°∠∠(两直线平行,同位角相等))。2××BC(等量代换)证法1:作BC的延长线CD,返回证法2:ABC过A作EFBA∥,ED∴∠B=BAE∠(两直线平行,内错角相等)∠C=CAD∠(两直线平行,内错角相等)又∵∠BAE+CAD+BAC=180°∠∠∴∠B+C+BAC=180°∠∠(平角的定义)(等量代换)返回在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线。在平面几何里,辅助线通常画成虚线。思路总结为了证明三个角的和为1800,转化为一个平角或同旁内角互补,这种转化思想是数学中的常用方法.三角形内角和定理:三角形的内角和等于1800.返回证法3:CBA过C作CDBA∥,D∴∠B=BCD∠(两直线平行,内错角相等)∠BCD+BAC+A=180°∠∠(两直线平行,同旁内角互补)∴∠B+BCA+A=180°∠∠(等量代换)返回(1)A∠=180°-_______;(2)B∠+∠C=180°-_______;引导学生对定理作出以下几种常用变形:3.已知:在△ABC中,∠C=∠ABC=2∠A,BD是AC边上的高。求∠DBC的度数。解:设∠A=x°,则∠C=∠ABC=2X0∴x+2x+2x=180解得:x=36°在△BDC中,∵∠BDC=90°∴∠DBC=180°-∠BDC-∠C=180°-90°-72°=180∴∠C=72°练习11△ABC中,若∠A+∠B=∠C,则△ABC是()A、锐角△B、直角△C、钝角△D、等腰△2一个三角形至少有()A、一个锐角B、两个锐角C、一个钝角D、一个直角3如图△ABC中,CD平分∠ACB,DEBC,A∥∠=70∠B=50,求∠BDC的度数。ABCDE动脑筋,你能行!例如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西40°方向。从C岛看A、B两岛的视角∠ACB是多少度?BECAD北北应用新知1、在△ABC中,(1)已知∠A=80°,能否求得∠B,∠C的度数?(2)已知∠A=80°,∠B=52°,则∠C=_。(3)已知∠A=80°,∠B-∠C=40°,则∠C=_。48°30°(4)已知∠A+∠B=100°,∠C=2∠A,则∠A=_、∠B=_、∠C=_。(5)已知∠A:∠B:∠C=1:2:3,则∠A=_、∠B=_、∠C=_,试判断△ABC的形状?(直角三角形)40°60°80°30°60°90°检验一下自己吧!1、在△ABC中,A=80°,B=C,∠∠∠求∠C的度数。解:在△ABC中,∠A+B+C=180°∠∠,∠A=80°∴∠B+C=100°∠∵∠B=C∠∴∠B=C=50∠0ABC2、已知三角形三个内角的度数之比为1:3:5,求这三个内角的度数。解:设三个内角度数分别为:x、3x、5x,由三角形内角和为180°得x+3x+5x=180°解得x=20°所以三个内角度数分别为20°,60°,100°。练习21如图△ABC中,∠ABC、∠ACB的平分线交于点O,⑴若∠A=70°,求∠BOC。⑵若∠A=X°,求∠BOC。ABCO动脑筋,你能行!作业.课本P76.复习巩固:3.4.中国首家新课标免费资源网(不必注册,免费下载)请记住我们的网址:www.kejian123.com