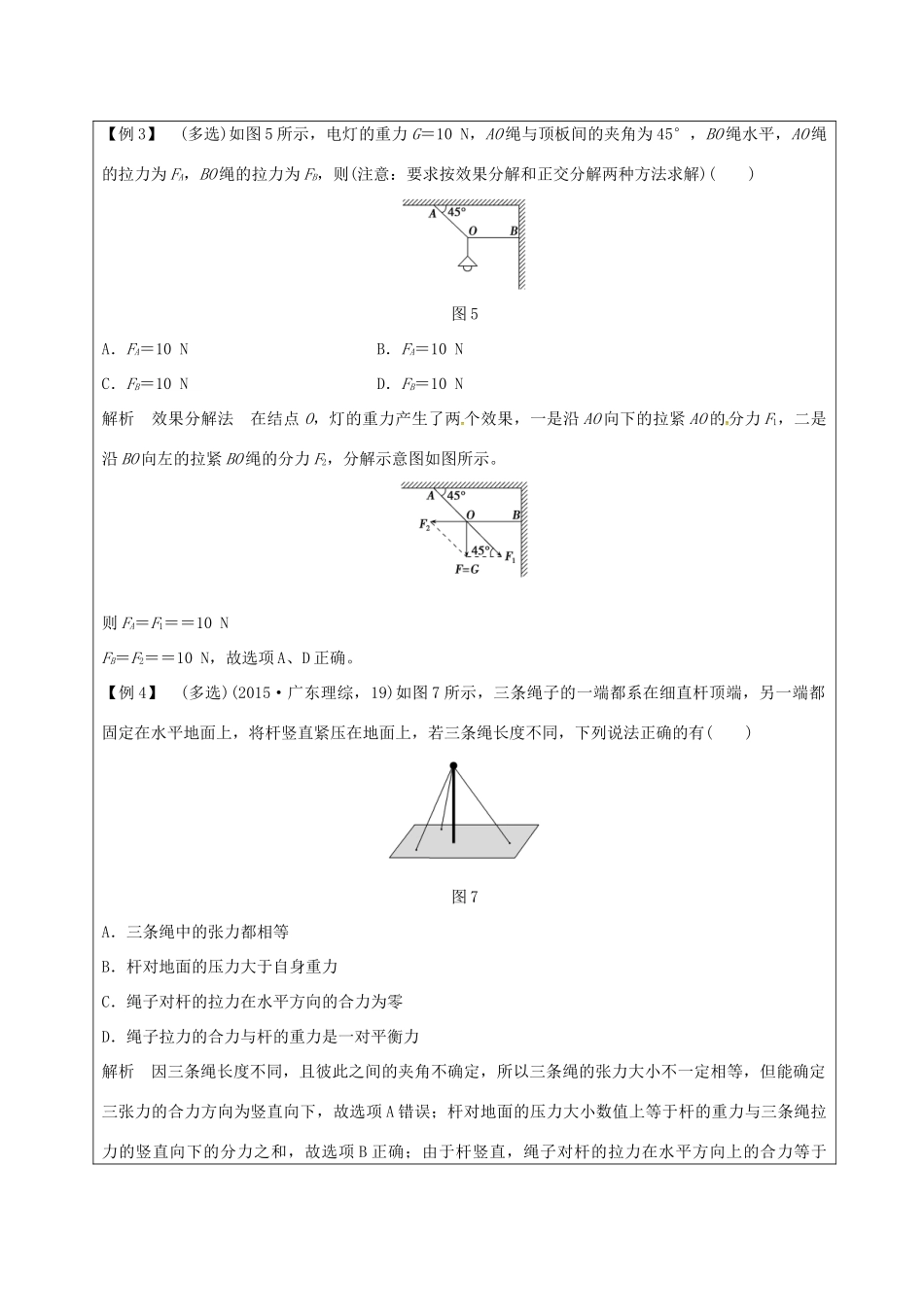
力的合成与分解课题力的合成与分解计划课时2节教学目标1、理解合力与分力的概念。2、理解共点力的概念3、掌握力的合成方法。4、掌握力的分解方法。教学重点力的合成与分解教学难点对实际问题进行正确的力的分解教学方法探究法、讨论法教学内容及教学过程一、引入课题物体往往会受到多个力的作用,如何求解物体所受的合力呢?二、主要教学过程知识点一、力的合成和分解1.合力与分力(1)定义:如果一个力产生的效果跟几个共点力共同作用产生的效果相同,这一个力就叫做那几个力的合力,原来的几个力叫做分力。(2)关系:合力和分力是等效替代的关系。2.共点力作用在物体的同一点,或作用线的延长线交于一点的力。3.力的合成(1)定义:求几个力的合力的过程。(2)运算法则①平行四边形定则:求两个互成角度的共点力的合力,可以用表示这两个力的线段为邻边作平行四边形,这两个邻边之间的对角线就表示合力的大小和方向。②三角形定则:把两个矢量首尾相接,从而求出合矢量的方法。图14.力的分解(1)定义:求一个已知力的分力的过程。(2)遵循原则:平行四边形定则或三角形定则。(3)分解方法:①按力产生的效果分解;②正交分解。知识点二、矢量和标量1.矢量:既有大小又有方向的量,相加时遵从平行四边形定则。2.标量:只有大小没有方向的量,求和时按代数法则相加。三、典型例题分析【例1】(多选)两个共点力F1、F2大小不同,它们的合力大小为F,则()A.F1、F2同时增大一倍,F也增大一倍B.F1、F2同时增加10N,F也增加10NC.F1增加10N,F2减少10N,F一定不变D.若F1、F2中的一个增大,F不一定增大解析F1、F2同时增大一倍,F也增大一倍,选项A正确;F1、F2同时增加10N,F不一定增加10N,选项B错误;F1增加10N,F2减少10N,F可能变化,选项C错误;若F1、F2中的一个增大,F不一定增大,选项D正确。【例2】一物体受到三个共面共点力F1、F2、F3的作用,三力的矢量关系如图4所示(小方格边长相等),则下列说法正确的是()图4A.三力的合力有最大值F1+F2+F3,方向不确定B.三力的合力有唯一值3F3,方向与F3同向C.三力的合力有唯一值2F3,方向与F3同向D.由题给条件无法求合力大小解析先以力F1和F2为邻边作平行四边形,其合力与F3共线,大小F12=2F3如图所示,合力F12再与第三个力F3合成求合力F合。可见F合=3F3。答案B【例3】(多选)如图5所示,电灯的重力G=10N,AO绳与顶板间的夹角为45°,BO绳水平,AO绳的拉力为FA,BO绳的拉力为FB,则(注意:要求按效果分解和正交分解两种方法求解)()图5A.FA=10NB.FA=10NC.FB=10ND.FB=10N解析效果分解法在结点O,灯的重力产生了两个效果,一是沿AO向下的拉紧AO的分力F1,二是沿BO向左的拉紧BO绳的分力F2,分解示意图如图所示。则FA=F1==10NFB=F2==10N,故选项A、D正确。【例4】(多选)(2015·广东理综,19)如图7所示,三条绳子的一端都系在细直杆顶端,另一端都固定在水平地面上,将杆竖直紧压在地面上,若三条绳长度不同,下列说法正确的有()图7A.三条绳中的张力都相等B.杆对地面的压力大于自身重力C.绳子对杆的拉力在水平方向的合力为零D.绳子拉力的合力与杆的重力是一对平衡力解析因三条绳长度不同,且彼此之间的夹角不确定,所以三条绳的张力大小不一定相等,但能确定三张力的合力方向为竖直向下,故选项A错误;杆对地面的压力大小数值上等于杆的重力与三条绳拉力的竖直向下的分力之和,故选项B正确;由于杆竖直,绳子对杆的拉力在水平方向上的合力等于零,故选项C正确;绳子拉力的合力方向与杆的重力方向均竖直向下,故两者不是一对平衡力,故选项D错误。答案BC四、课堂练习《创新设计》第22、23页变式训练1、2、3、五、课堂小结力的分解常用的方法正交分解法效果分解法分解方法将一个力沿着两个互相垂直的方向进行分解的方法根据一个力产生的实际效果进行分解的方法实例分析x轴方向上的分力:Fx=Fcosθy轴方向上的分力:Fy=FsinθF1=F2=Gtanθ六、作业《4级优化满分练》第二章基础课时5板书设计力的合成与分解一、力的合成和分解二、力的合成1.合力与分力(1)定义(1)定义:(2)遵循原则(2)关系:(3)分解方法2.共点力教学反思学生对典型问题,如斜面上重力的分解,已知合力大小及一个力的方向,求解另一个力的极值问题掌握不到位,需进一步加强。