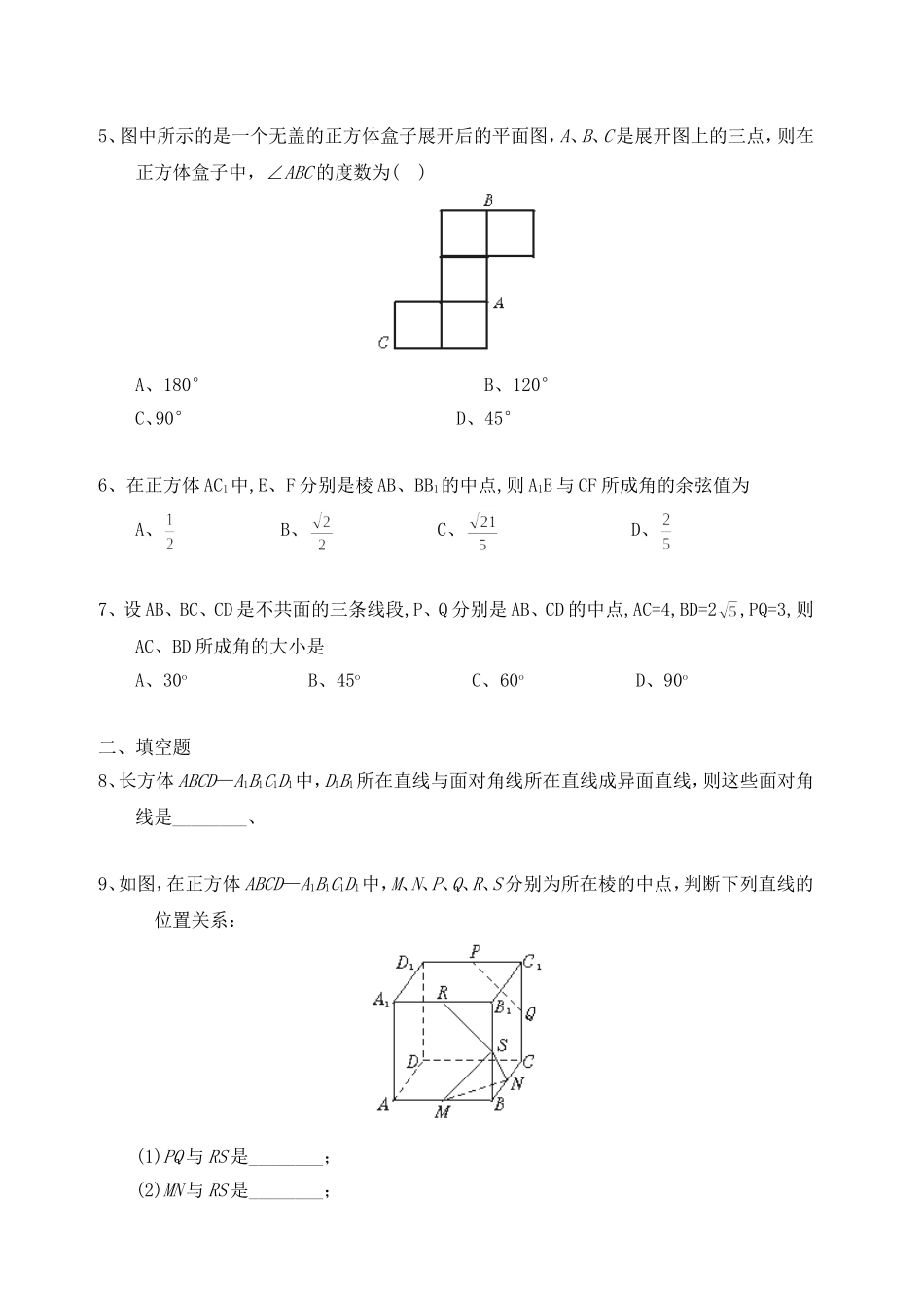
2、1、2空间中直线与直线之间的位置关系练习二一、选择题1、已知直线a、b是异面直线,且a平面,b平面,平面∩平面=c,那么直线c()A、同时与a、b相交B、至多与a、b中的一条相交C、与a、b中的一条相交,另一条平行D、至少和a、b中的一条相交2、下列命题中,结论正确的个数是()①如果一个角的两边与另一个角的两边分别平行,那么这两个角相等②如果两条相交直线和另外两条相交直线分别平行,那么这两组直线所成的锐角或直角相等③如果一个角的两边与另一个角的两边分别垂直,那么这两个角相等或互补④如果两条直线同时平行于第三条直线,那么这两条直线互相平行A、1B、2C、3D、43、已知异面直线a与b所成的角是60°,P为空间中的一个定点,则过点P与a、b所成的角都是60°的直线有()A、3条B、4条C、5条D、6条4、如图,立体图形S—ABC中,SA=SB=SC=AB=AC=BC,如果E、F分别为SA、BC的中点,那么异面直线EF与SC所成的角等于()A、90°B、60°C、45°D、30°5、图中所示的是一个无盖的正方体盒子展开后的平面图,A、B、C是展开图上的三点,则在正方体盒子中,∠ABC的度数为()A、180°B、120°C、90°D、45°6、在正方体AC1中,E、F分别是棱AB、BB1的中点,则A1E与CF所成角的余弦值为A、B、C、D、7、设AB、BC、CD是不共面的三条线段,P、Q分别是AB、CD的中点,AC=4,BD=2,PQ=3,则AC、BD所成角的大小是A、30oB、45oC、60oD、90o二、填空题8、长方体ABCD—A1B1C1D1中,D1B1所在直线与面对角线所在直线成异面直线,则这些面对角线是________、9、如图,在正方体ABCD—A1B1C1D1中,M、N、P、Q、R、S分别为所在棱的中点,判断下列直线的位置关系:(1)PQ与RS是________;(2)MN与RS是________;(3)PQ与MN是________10、如图,在正方体ABCD—A1B1C1D1中,M、N、P、Q、R、S分别是各点所在棱的中点,则PQ和RS的位置关系是________;MN和RS的位置关系是________;它们所成的角是________;PQ和MN的位置关系是相交;它们所成的角是________11、如图,在正四面体A—BCD(各面都是正三角形)中,面ABC的中心是O1,面ADC的中心是O2,则AB与O1O2所成的角的大小是________12、下图为正方体平面展开图,那么在正方体中,有以下四个结论:(1)BM与ED平行;(2)CN与BE是异面直线;(3)CN与BM成60°;(4)DN⊥FN以上四个结论中,正确结论的序号是________(写出所有情况)三、解答题13、空间四边形ABCD,AB≠AC,AE是△ABC的边BC上的高,DF是△BCD的BC边上的中线,求证:AE和DF是异面直线14、空间四边形ABCD中,P、Q、R、S分别是四条边AB、BC、CD、DA的中点,已知AC=12,BD=4,且四边形PQRS的面积是12,求异面直线AC、BD所成的角15、如图,空间四边形ABCD中,两条对边AB=CD=3,E、F分别是另外两条对边AD、BC上的点,且AE∶ED=BF∶FC=1∶2,EF=,求AB和CD所成角的正切值答案:一、选择题1.D;2、B;3、A;4、C;5、C;6、D;7、D二、填空题8、C1D、BC1、A1B、A1D、AC9、(1)平行直线(2)异面直线(3)相交直线10、平行异面60°60°11、60°12、(3)、(4)三、解答题13、证明:若AE和DF不是异面直线,则AE与DF共面,设过AE、DF的平面为、(1)若E、F重合,则E是BC中点,这与题设AB≠AC相矛盾;(2)若E、F不重合,∵B∈EF,C∈EF,EF∴BC∵A∈,D∈∴A、B、C、D四点共面,这与题设ABCD是空间四边形相矛盾、由(1)、(2)可知,AE和DF不是异面直线不成立∴AE和DF是异面直线、14、解:∵P、Q、R、S是四边AB、BC、CD、DA的中点,∴SR∥AC,QR∥BD∴QR、SR所成的角,就是BD与AC所成的角、∵AC=12,BD=4∴SR=6,QR=2S四边形PQRS=SR·QR·sin∠SRQ=6·2·sin∠SRQ=12sin∠SRQ又S四边形PQRS=12∴12sin∠SRQ=12∴sin∠SRQ=∴∠SRQ=45°或135°∴SR与RQ所成的角为45°,即AC、BD所成的角为45°、15、解:连结BD,作EG∥AB,交BD于点G,连结GF,则=、又=,∴=∴GF∥DC∴EG与GF所成的角就是AB与CD所成的角、在△EGF中,EG=AB=2,GF=CD=1,EF=,由余弦定理,得cos∠EGF==-∴∠EGF=120°∴AB与CD所成的角为60°∴AB与CD所成角的正切值为、