2015年下期高中数学综合训练1VIP免费

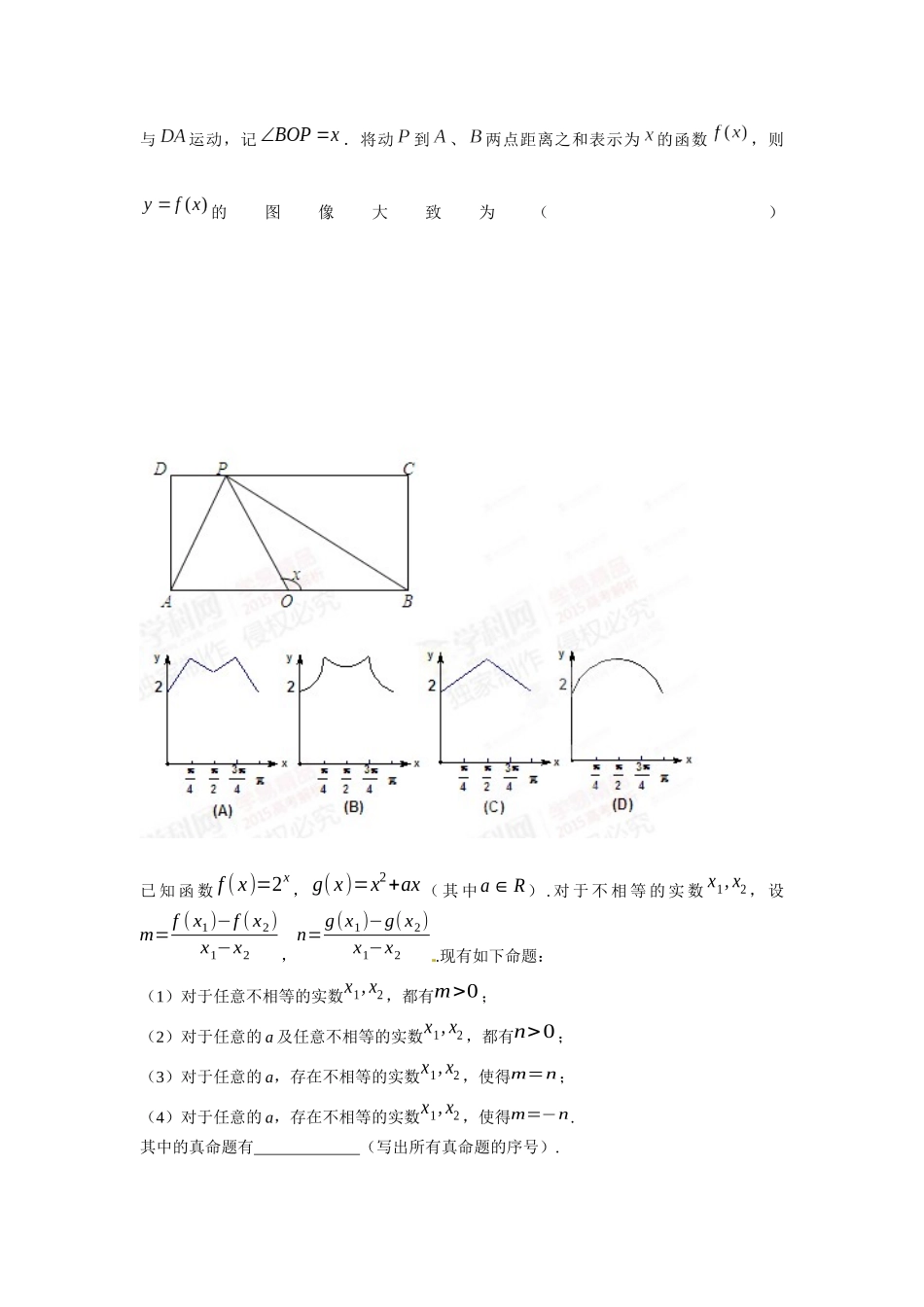
2015年高中数学综合训练1在等差数列中，若，则=.中位数1010的一组数构成等差数列，其末项为2015，则该数列的首项为．已知是等差数列，公差不为零，前项和是，若，，成等比数列，则（）A.B.C.D.已知数列是递增的等比数列，，则数列的前项和等于.设是数列的前n项和，且，，则________．数列}{na满足11a，且11naann（*Nn），则数列}1{na的前10项和为。设是各项为正数且公差为d的等差数列（1）证明：依次成等比数列；（2）是否存在，使得依次成等比数列，并说明理由已知函数．（Ⅰ）求曲线在点处的切线方程；（Ⅱ）求证：当时，；（Ⅲ）设实数使得对恒成立，求的最大值．【2015高考山东，理21】设函数，其中.na2576543aaaaa82aa（Ⅰ）讨论函数极值点的个数，并说明理由；（Ⅱ）若成立，求的取值范围.已知数列的各项均为正数，，e为自然对数的底数．（Ⅰ）求函数的单调区间，并比较与e的大小；（Ⅱ）计算，，，由此推测计算的公式，并给出证明；（Ⅲ）令，数列，的前项和分别记为,,证明：.已知函数，其中.(I)讨论的单调性；(II)设曲线与轴正半轴的交点为P，曲线在点P处的切线方程为,求证：对于任意的正实数，都有；(III)若关于的方程有两个正实根，求证：设，其中均为实数，下列条件中，使得该三次方程仅有一个实根的是.（写出所有正确条件的编号）①；②；③；④；⑤.如图，长方形的边，，是的中点，点沿着边，nneST与运动，记．将动到、两点距离之和表示为的函数，则的图像大致为（）已知函数f(x)=2x，g(x)=x2+ax（其中a∈R）.对于不相等的实数x1,x2，设m=f(x1)−f(x2)x1−x2，n=g(x1)−g(x2)x1−x2.现有如下命题：（1）对于任意不相等的实数x1,x2，都有m>0；（2）对于任意的a及任意不相等的实数x1,x2，都有n>0；（3）对于任意的a，存在不相等的实数x1,x2，使得m=n；（4）对于任意的a，存在不相等的实数x1,x2，使得m=−n.其中的真命题有（写出所有真命题的序号）.在ABC中，B=，AB=，A的角平分线AD=,则AC=_______.在中，内角，，所对的边分别为，，，已知，=.（1）求的值；（2）若的面积为7，求的值.在平面四边形ABCD中，∠A=∠B=∠C=75°，BC=2，则AB的取值范围是.中，是上的点，平分，面积是面积的2倍．(Ⅰ)求；(Ⅱ)若，，求和的长