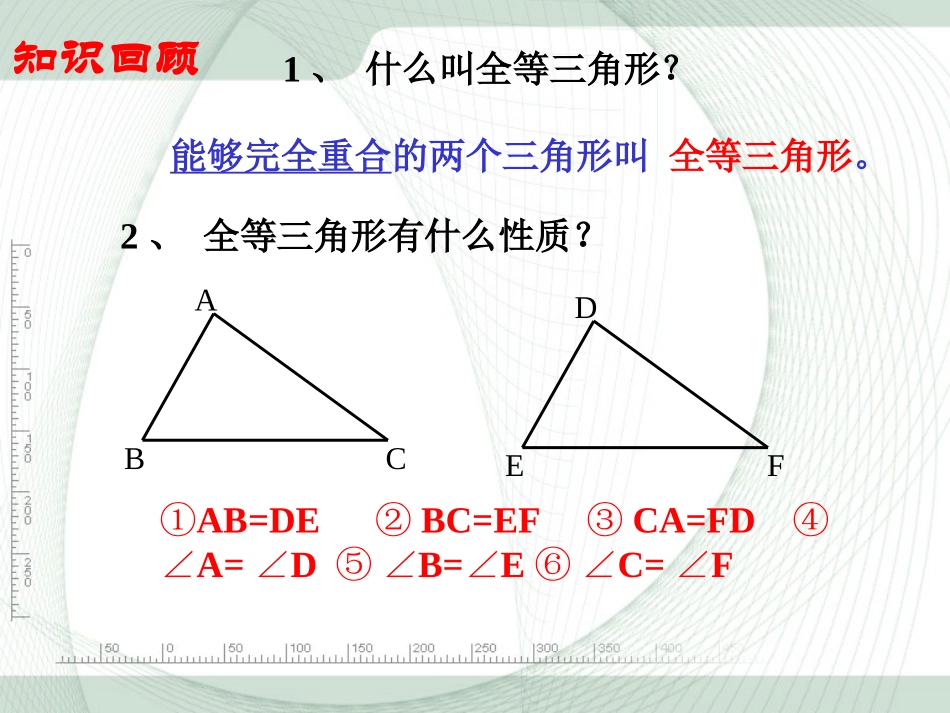
12.2三角形全等的判定(1)①AB=DEBC=EFCA=FD②③④A=DB=EC=F∠∠⑤∠∠⑥∠∠ABCDEF1、什么叫全等三角形?能够完全重合的两个三角形叫全等三角形。2、全等三角形有什么性质?知识回顾情境问题:小明家的衣橱上镶有两块全等的三角形玻璃装饰物,其中一块被打碎了,妈妈让小明到玻璃店配一块回来,请你说说小明该怎么办?1.只给一个条件(一组对应边相等或一组对应角相等)。①只给一条边:②只给一个角:60°60°60°探究:2.给出两个条件:①一边一内角:②两内角:③两边:30°30°30°30°30°50°50°2cm2cm4cm4cm可以发现按这些条件画的三角形都不能保证一定全等。三边对应相等的两个三角形全等(可以简写为“边边边”或“SSS”)。已知三角形三条边分别是4cm,5cm,7cm,画出这个三角形,把所画的三角形分别剪下来,并与同伴比一比,发现什么?探究新知思考:你能用“边边边”解释三角形具有稳定性吗?判断两个三角形全等的推理过程,叫做证明三角形全等。AB=DEBC=EFCA=FDABCDEF用数学语言表述:在△ABC和△DEF中∴△ABCDEF≌△(SSS){例1.如下图,△ABC是一个刚架,AB=AC,AD是连接A与BC中点D的支架。求证:△ABDACD≌△分析:要证明△ABDACD≌△,首先看这两个三角形的三条边是否对应相等。结论:从这题的证明中可以看出,证明是由题设(已知)出发,经过一步步的推理,最后推出结论正确的过程。应用迁移①准备条件:证全等时要用的间接条件要先证好;②三角形全等书写三步骤:1.写出在哪两个三角形中2.摆出三个条件用大括号括起来3.写出全等结论证明的书写步骤:归纳1.已知AC=FE,BC=DE,点A,D,B,F在一条直线上,AD=FB(如图),要用“边边边”证明△ABCFDE≌△,除了已知中的AC=FE,BC=DE以外,还应该有什么条件?怎样才能得到这个条件?解:要证明△ABCFDE≌△,还应该有AB=DF这个条件∵DB是AB与DF的公共部分,且AD=BF∴AD+DB=BF+DB即AB=DF练一练2.如图,AB=AC,AE=AD,BD=CE,求证:△AEBADC≌△。证明:∵BD=CE∴BD-ED=CE-ED,即BE=CD。在AEB和ADC中,AB=ACAE=ADBE=CD∴△AEBADC≌△CABDE{3、如图,在四边形ABCD中,AB=CD,AD=CB,求证:∠A=∠C.DABC•证明:在△ABD和△CDB中AB=CDAD=CBBD=DB∴△ABDACD≌△(SSS)(已知)(已知)(公共边)∴∠A=C∠(全等三角形的对应角相等)你能说明ABCD∥,ADBC∥吗?4、如图,AB=AC,BD=CD,BH=CH,图中有几组全等的三角形?它们全等的条件是什么?HDCBA解:有三组。在△ABH和△ACH中∵AB=AC,BH=CH,AH=AH∴△ABHACH≌△(SSS);∵BD=CD,BH=CH,DH=DH∴△DBHDCH≌△(SSS)在△ABH和△ACH中∵AB=AC,BD=CD,AD=AD∴△ABDACD≌△(SSS);在△ABH和△ACH中解:①∵E、F分别是AB,CD的中点()又∵AB=CD∴AE=CF在△ADE与△CBF中AE==∴△ADECBF()≌△∴AE=ABCF=CD()1212补充练习:如图,已知AB=CD,AD=CB,E、F分别是AB,CD的中点,且DE=BF,说出下列判断成立的理由.①△ADECBF≌△②∠A=C∠线段中点的定义CFADABCDSSS△ADECBF≌△全等三角形对应角相等已知ADBCFECB②∵∴∠A=C()∠=BCBCBCBC△DCB△DCBBF=DCBF=DC或BD=FC或BD=FCAABBCCDD解:△ABC≌DCB△理由如下:AB=CDAC=BD=解:△ABC≌DCB△理由如下:AB=CDAC=BD=△ABD≌()△ABD≌()SSSSSS如图,AB=CD,AC=BD,△ABC和△DCB是否全等?试说明理由。如图,AB=CD,AC=BD,△ABC和△DCB是否全等?试说明理由。(2)如图,D、F是线段BC上的两点,AB=CE,AF=DE,要使△ABF≌△ECD,还需要条件?(2)如图,D、F是线段BC上的两点,AB=CE,AF=DE,要使△ABF≌△ECD,还需要条件?AAEEBDFCBDFC小结2.三边对应相等的两个三角形全等(边边边或SSS);3.书写格式:①准备条件;②三角形全等书写的三步骤。1.知道三角形三条边的长度怎样画三角形。•习题12.2复习巩固1、2.作业布置