【课堂新坐标】2013届高考数学一轮复习-第三章第二节-同角三角函数的基本关系与诱导公式课件-理-(广东专用VIP免费

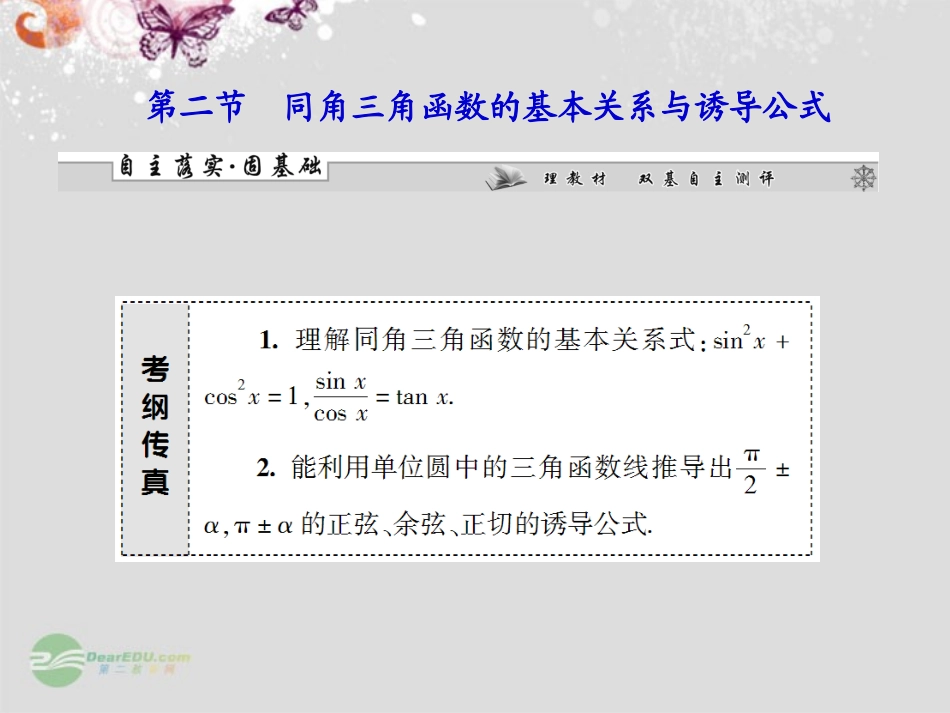
第二节同角三角函数的基本关系与诱导公式1．同角三角函数的基本关系2．诱导公式组数一二三四五六角2kπ＋α(k∈Z)π＋α－απ－α正弦sinα_____________________________－sinα－sinα－sinαcosαcosα余弦cosα_________________________________正切tanα_____________________口诀函数名不变符号看象限函数名改变符号看象限－cosαcosα－cosαsinα－sinα－tanα－tanαtanα1．有人说sin(kπ－α)＝sin(π－α)＝sinα(k∈Z)，你认为正确吗？【提示】不正确．当k＝2n(n∈Z)时，sin(kπ－α)＝sin(2nπ－α)＝－sinα；当k＝2n＋1(n∈Z)时，sin(kπ－α)＝sin(2nπ＋π－α)＝sin(π－α)＝sinα.2．诱导公式可统一为“奇变偶不变，符号看象限”，这里的“奇、偶”指π2的奇数倍或偶数倍，那么“符号”的含义是什么？【提示】是指把“α”看作锐角时，原三角函数值的符号．1．(教材改编题)已知cos(α－π)＝－513，且α是第四象限角，则sinα＝()A．－1213B.1213C.512D．±1213【解析】 cos(α－π)＝cos(π－α)＝－cosα＝－513，∴cosα＝513，又α是第四象限角，∴sinα＜0，则sinα＝－1－cos2α＝－1213.【答案】A2．sin43π·cos56π·tan(－43π)的值是()A．－334B.334C．－34D.34【解析】原式＝sin(π＋π3)·cos(π－π6)·tan(－π－π3)＝(－sinπ3)·(－cosπ6)·(－tanπ3)＝(－32)×(－32)×(－3)＝－334.【答案】A3．(2011·福建高考)若tanα＝3，则sin2αcos2α的值等于()A．2B．3C．4D．6【解析】sin2αcos2α＝2sinαcosαcos2α＝2tanα，又tanα＝3，∴sin2αcos2α＝2×3＝6.【答案】D4．已知α是第二象限角，tanα＝－12，则cosα＝________.【解析】由题意得cosα＝－11＋tan2α＝－255.【答案】－255【思路点拨】(1)利用商数关系与平方关系；(2)由条件可求cosα，进而求sinα与tanα.同角三角函数关系式的应用(1)(2011·全国卷改编)已知α∈(π，32π)，tanα＝2，则sinα＝________.(2)(2011·福建高考)若α∈(0，π2)，且sin2α＋cos2α＝14，则tanα的值等于()A.22B.33C.2D.3【尝试解答】(1) α∈(π，32π)，且tanα＝2，∴sinα＝2cosα＜0，又sin2α＋cos2α＝1，∴sin2α＝45，sinα＝－255.(2) sin2α＋cos2α＝14，∴sin2α＋cos2α－sin2α＝14，则cos2α＝14.∴sin2α＝1－cos2α＝34，则tan2α＝3.又α∈(0，π2)，因此tanα＝3.【答案】(1)－255(2)D1．两题是同角关系式的基本题，求解的原则：“先平方，后作商”，第(2)小题亦可先求出α＝π3，然后利用特殊角的三角函数值求解．2．若题目中α的范围不能确定，开方时应注意讨论三角函数值的符号．已知cos(π＋x)＝35，x∈(π，2π)，则tanx等于()A．－34B．－43C.34D.43【解析】由cos(π＋x)＝35，得cosx＝－35，又x∈(π，2π)，得sinx＜0，∴sinx＝－1－cos2x＝－45.因此tanx＝sinxcosx＝43.【答案】D【思路点拨】由诱导公式，化同角α的三角函数，再运用同角三角函数关系式化简，求值．诱导公式的应用已知f(α)＝sinπ－αcos2π－αtan－α＋π－tan－α－πsin－π－α，(1)化简f(α)；(2)若α是第三象限角，且cos(α－3π2)＝15，求f(α)的值．【尝试解答】(1)f(α)＝sinα·cosα·－tanαtanα＋π[－sinπ＋α]＝－sinα·cosα·tanαtanα·sinα＝－cosα.(2) cos(α－32π)＝cos(32π－α)＝－sinα.∴sinα＝－15.又α是第三象限角，∴cosα＜0.∴cosα＝－1－sin2α＝－256.因此f(α)＝－cosα＝256.1．熟练运用诱导公式是解答本题的关键．(1)诱导公式除了正面用于化简外，还应掌握它的逆向应用，从角的形式上分析出两角之间的关系；(2)诱导公式的应用原则：负化正、大化小，化到锐角或已知角为止．2．解题时注意已知角或函数名称与所求角或三角函数名称之间存在的关系，选择恰当的公式，要向所求角和三角函数进行化归．已知sinα＝－255，且tanα＜0.(1)求tanα；(2)求2sinπ＋α＋cos2π－αcosα－π2－sin3π2＋α.【解】(1)由sinα＝－255，且tanα＜0，所以cosα＞0，则cosα＝1－sin2α＝55，∴tanα...