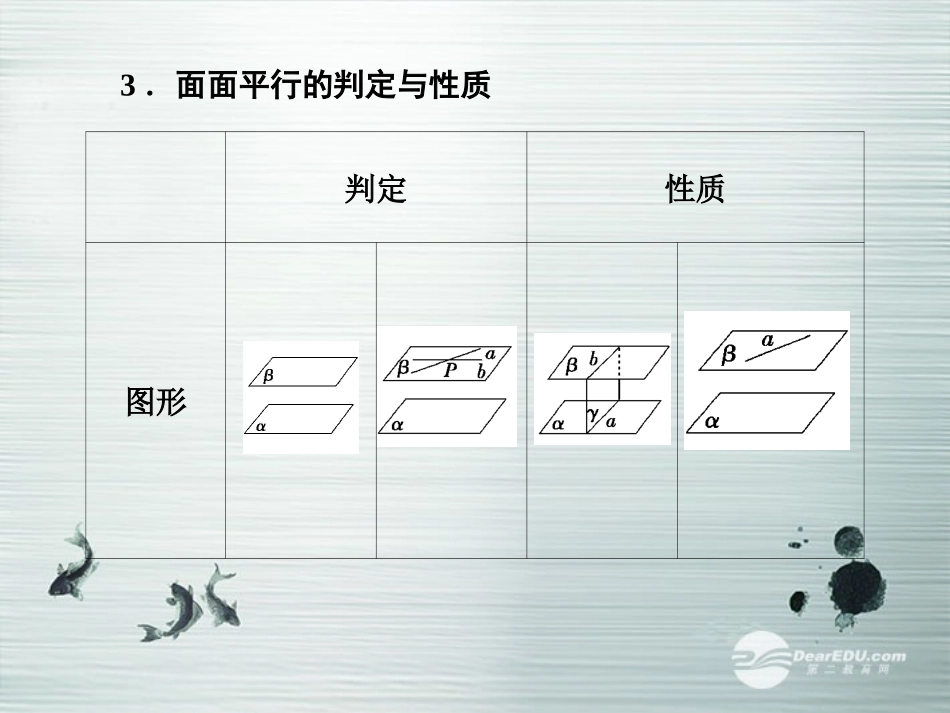
第四节直线、平面平行的判定及其性质1.直线与平面平行的判定(1)定义:直线与平面___________,则称直线平行于平面.(2)判定定理:若____________________,则bα.∥2.直线与平面平行的性质定理若______________________________,则ab.∥没有公共点3.面面平行的判定与性质判定性质图形1.如果两个平面平行,则一个平面内的直线与另一个平面内的直线有哪些位置关系?【提示】平行或异面.2.如果一个平面内有无数条直线平行于另一个平面,那么这两个平面一定平行吗?【提示】不一定.可能平行也可能相交.1.(人教A版教材习题改编)若直线a不平行于平面α,则下列结论成立的是()A.α内的所有直线都与直线a异面B.α内可能存在与a平行的直线C.α内的直线都与a相交D.直线a与平面α没有公共点【解析】直线a与α不平行,则直线a在α内或与α相交,当直线a在平面α内时,在α内存在与a平行的直线,B正确.【答案】B2.若直线m平面α,则条件甲:直线lα∥,是条件乙:lm∥的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【解析】 lα∥时,l与m并不一定平行,而lm∥时,l与α也不一定平行,有可能lα,∴条件甲是条件乙的既不充分也不必要条件.【答案】D3.在正方体ABCD—A1B1C1D1中,E是DD1的中点,则BD1与平面ACE的位置关系是________.【解析】如图所示,连接BD交AC于F,连接EF则EF是△BDD1的中位线,∴EFBD∥1,又EF平面ACE,BD1平面ACE,∴BD1∥平面ACE.【答案】平行4.(2013·湛江模拟)如图7-4-1,正方体ABCD—A1B1C1D1中,AB=2,点E为AD的中点,点F在CD上.若EF∥平面AB1C,则线段EF的长度等于________.【解析】由于在正方体ABCD—A1B1C1D1中,AB=2,∴AC=22.又E为AD中点,EF∥平面AB1C,EF平面ADC,平面ADC∩平面AB1C=AC,∴EF∥AC,∴F为DC中点,∴EF=12AC=2.【答案】2(2012·辽宁高考)如图7-4-2,直三棱柱ABC-A′B′C′,∠BAC=90°,AB=AC=,AA′=1,点M,N分别为A′B和B′C′的中点.(1)证明:MN∥平面A′ACC′;(2)求三棱锥A′-MNC的体积.(锥体体积公式V=Sh,其中S为底面面积,h为高)【思路点拨】(1)法一:证明MN∥AC′;法二:取A′B′的中点P,证平面MPN∥平面A′ACC′.(2)转化法:根据S△A′MC=S△BMC得VN—A′MC=12VN—A′BC,从而VA′—MNC=12VA′—NBC.【尝试解答】(1)法一连接AB′,AC′,如图,由已知∠BAC=90°,AB=AC,三棱柱ABC—A′B′C′为直三棱柱,所以M为AB′的中点.又因为N为B′C′的中点,所以MNAC′.∥又MN平面A′ACC′,AC′平面A′ACC′,所以MN∥平面A′ACC′.法二取A′B′的中点P,连接MP,NP,AB′,如图.因为M,N分别为AB′与B′C′的中点,所以MPAA′∥,PNA′C′.∥所以MP∥平面A′ACC′,PN∥平面A′ACC′.又MP∩NP=P,所以平面MPN∥平面A′ACC′.而MN平面MPN,所以MN∥平面A′ACC′.(2)连接BN,由题意知,A′N⊥B′C′,平面A′B′C′∩平面B′BCC′=B′C′,所以A′N⊥平面B′BCC′,即A′N⊥平面NBC,故VA′—MNC=VN—A′MC=13S△A′MC×h,又S△A′MC=12S△A′BC,所以VA′—MNC=VN—A′MC=12VN—A′BC=12VA′—NBC=12×13×S△NBC×A′N,因为∠BAC=90°,BA=AC=2,所以BC=B′C′=2,S△NBC=12BC×BB′=12×2×1=1,A′N=12B′C′=1,所以VA′—MNC=VN—A′MC=12×13×S△NBC×A′N=16.如图7-4-3,四边形ABCD是平行四边形,点P是平面ABCD外一点,M是PC的中点,在DM上取一点G,过G和AP作平面交平面BDM于GH.求证:APGH.∥【证明】如图,连接AC交BD于O,连接MO, 四边形ABCD是平行四边形,∴O是AC中点,又M是PC的中点,∴APOM∥,则有PA∥平面BMD. 平面PAHG∩平面BMD=GH,∴PA∥GH.如图7-4-4,已知αβ∥,异面直线AB、CD和平面α、β分别交于A、B、C、D四点,E、F、G、H分别是AB、BC、CD、DA的中点.求证:(1)E、F、G、H共面;(2)平面EFGH∥平面α.【思路点拨】(1)证明四边形EFGH为平行四边形即可;(2)利用面面平行的判定定理,转化为线面平行来证明.【尝试解答】(1) E、H分别是AB、DA的中点,∴EH綊12BD.同理,FG綊12BD,∴F...