14.2三角形全等的判定一VIP免费

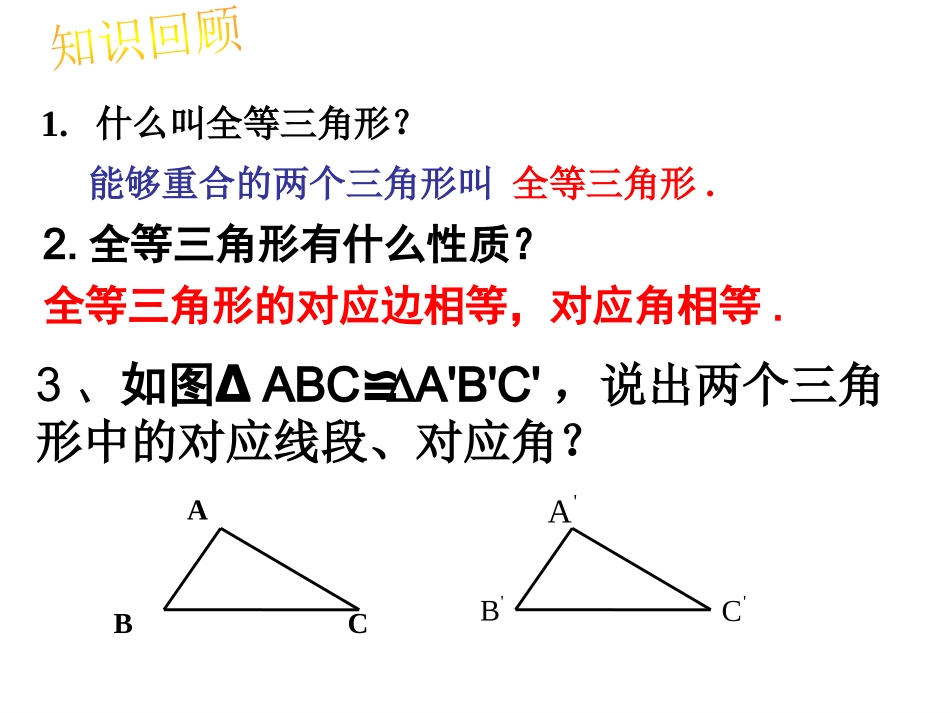
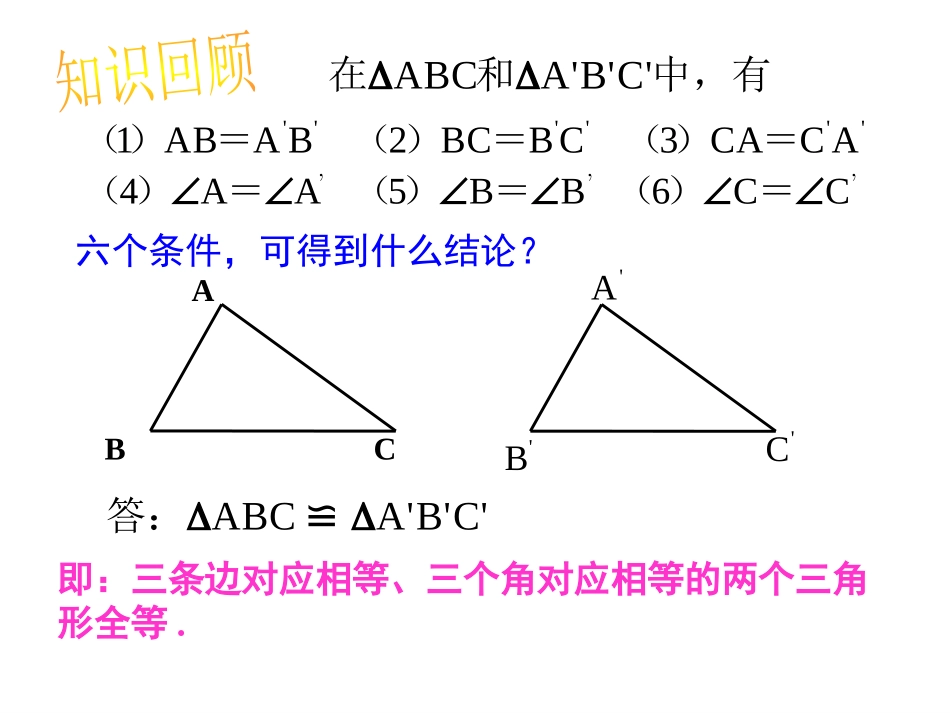
14.2三角形全等的判定1（边角边---SAS）ABC1.什么叫全等三角形？能够重合的两个三角形叫全等三角形.2.全等三角形有什么性质？全等三角形的对应边相等，对应角相等.3、如图∆ABC∆A'B'C'≌，说出两个三角形中的对应线段、对应角？'A'B'CABC即：三条边对应相等、三个角对应相等的两个三角形全等.六个条件，可得到什么结论？'A'B'CC'B'A'ABC答：≌''''''ACCA3CBBC2BAAB1＝）（＝）（＝）（C'B'A'ABC中，有和在CC6BB5AA4＝）（＝）（＝）（’’’与满足上述六个条件中的一部分是否能保证与全等呢？CBAABCCBAABCABCABC一个条件可以吗？两个条件可以吗？一个条件可以吗？1.有一条边相等的两个三角形不一定全等探究活动2.有一个角相等的两个三角形不一定全等结论：有一个条件相等不能保证两个三角形全等.6cm300有两个条件对应相等不能保证三角形全等.60o300不一定全等1.有两个角对应相等的两个三角形两个条件可以吗？3.有一个角和一条边对应相等的两个三角形2.有两条边对应相等的两个三角形4cm6cm不一定全等30060o4cm6cm不一定全等30o6cm结论：探究活动三个条件呢？探究活动1.三个角；2.三条边；3.两边一角；4.两角一边.如果给出三个条件画三角形，你能说出有哪几种可能的情况？尺规作图，探究边角边的判定方法已知：△ABC，求作：△A′B′C′，使A′B′=AB，∠B＇=∠B，B′C′=BC（即两边和它们的夹角分别相等）．把画好的△A′B′C′剪下来，放到△ABC上，它们全等吗？BCAABCA′DE尺规作图，探究边角边的判定方法现象：两个三角形放在一起能完全重合．说明：这两个三角形全等．画法：（1）画∠DA′E=∠A；（2）在射线A′D上截取A′B′=AB，在射线A′E上截取A′C′=AC；（3）连接B′C′．B′C′几何语言：在△ABC和△A′B′C′中，∴△ABC≌△A′B′C′（SAS）．尺规作图，探究边角边的判定方法归纳概括“SAS”判定方法:两边及其夹角分别相等的两个三角形全等（可简写成“边角边”或“SAS”）．AB=A′B′，∠A=∠A′，AC=A′C′，课堂练习下列图形中有没有全等三角形，并说明全等的理由．甲8cm9cm丙8cm9cm8cm9cm乙30°30°30°课堂练习图甲与图丙全等，依据就是“SAS”，而图乙中30°的角不是已知两边的夹角，所以不与另外两个三角形全等．甲8cm9cm丙8cm9cm8cm9cm乙30°30°30°已知：如图，AD∥BC，AD=CB求证：△ADCCBA≌△分析：观察图形，结合已知条件，知，AD=CB，AC=CA，但没有给出两组对应边的夹角（∠1，∠2）相等.所以，应设法先证明∠1=∠2，才能使全等条件充足.AD=CB（已知）∠1=2∠（已证）AC=CA（公共边）∴△ADCCBA≌△（SAS）例1:证明：∵ADBC∥∴∠1=2∠（两直线平行，内错角相等）在△DAC和△BCA中DC1AB2B范例学习范例学习例2:如图，在湖泊的岸边有A、B两点，难以直接量出A、B两点间的距离.你能设计一种量出A、B两点之间距离的方案吗？说明你这样设计的理由.。AB范例学习范例学习小明的设计方案：先在池塘旁取一个能直接到达A和B处的点C，连结AC并延长至D点，使AC=DC，连结BC并延长至E点，使BC=EC，连结DE，量出DE的长，这个长度就是A，B两点的距离.AC=DC∠ACB=DCE∠BC=EC∴△ACBDCE△∴AB=DE在△ACB和△DCE中理由：１：如图，已知AB和CD相交与O,OA=OB,OC=OD,说明△OAD与△OBC全等的理由.OA=OB(已知）∠1=2∠（对顶角相等）OD=OC（已知）∴△OADOBC(SAS)≌△解：在△OAD和△OBC中CBADO21巩固练习2.如图所示,根据题目条件，判断下面的三角形是否全等．（1）AC＝DF，∠C＝∠F，BC＝EF；（2）BC＝BD，∠ABC＝∠ABD．答案:(1)全等(2)全等巩固练习BCDEA练习3：如图，已知AB＝AC，AD＝AE.求证：∠B＝∠CCEABAD证明：在△ABD和△ACE中（已知）＝（公共角）＝（已知）＝AEADAAACAB∴△ABDACE≌△（SAS）∴∠B＝∠C（全等三角形对应角相等）练习4：已知:如图,AB=DB,CB=EB,1∠＝∠2求证:A=D∠∠证明:1∵∠＝∠2(已知)∴∠1+DBC∠＝∠2+DBC∠(等式的性质)即∠ABC＝∠DBE在△ABC和△DBE中,AB＝DB(已知)∠ABC＝∠DBE(已证)CB＝EB(已知)∴△ABCDBE(SAS)≌△∴∠A=D(∠全等三角形的对应角相等)1A2CBDE1、本节课学习了哪些主要内容？2、我们是怎么探究出“SAS”判定方法的？用“SAS”判定三角形全等应注意什么问题？课堂小结•课本P100练习2、3课外：《基础训练》14.2第1课时布置作业