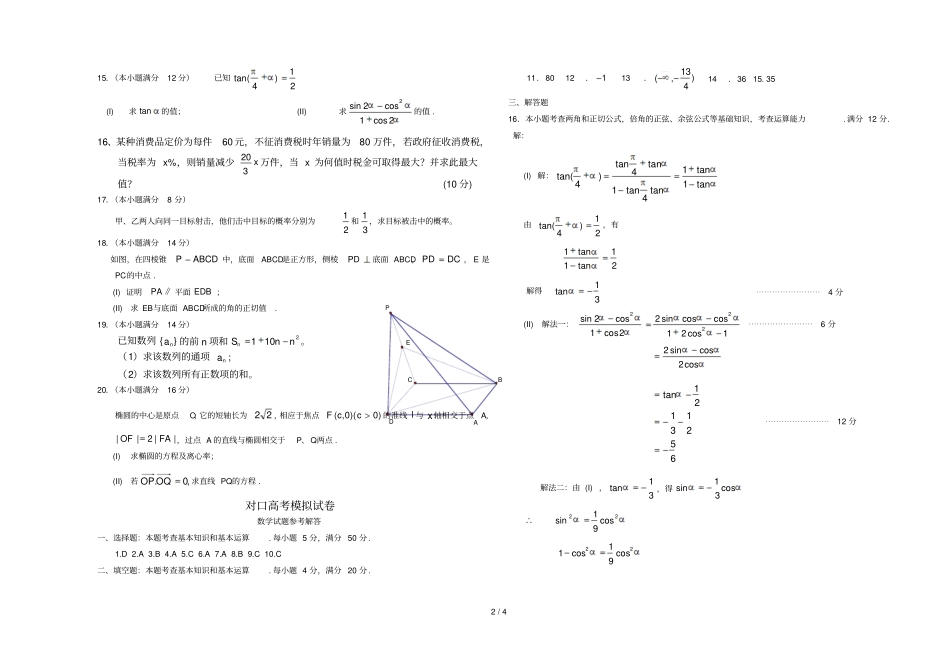
1/4对口高考数学模拟试卷本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分,考试用时120分钟.第Ⅰ卷(选择题共50分)参考公式:如果事件A、B互斥,那么柱体(棱柱、圆柱)的体积公式P(A+B)=P(A)+P(B)hVS柱体如果事件A、B相互独立,那么其中S表示柱体的底面积,P(A·B)=P(A)·P(B)h表示柱体的高一、单项选择题:(每一小题仅有一个正确答案,请将正确答案的代号填入答题表内。每小题5分,共计60分)1.下列关系中正确的是()A.0B.a{a}C.{a,b}{b,a}D.}0{2.不等式21xx的解集为()A.)0,1[B.),1[C.]1,(D.),0(]1,(3.对任意实数,,abc在下列命题中,真命题是()A.""acbc是""ab的必要条件B.""acbc是""ab的必要条件C.""acbc是""ab的充分条件D.""acbc是""ab的充分条件4.若平面向量b与向量)2,1(a的夹角是o180,且53||b,则b()A.)6,3(B.)6,3(C.)3,6(D.)3,6(5.设P是双曲线19222yax上一点,双曲线的一条渐近线方程为023yx,1F、2F分别是双曲线的左、右焦点。若3||1PF,则||2PF()A.1或5B.6C.7D.96、原点到直线y=kx+2的距离为2,则k的值为()A.1B.-1C.1D.77、若135sin)cos(cos)sin(,且是第二象限角,则cos的值为()A.1312B.1312C.53D.538、在等差数列{an}中,a1+a2+a3+a4+a5=15,a3=()A.2B.3C.4D.59、已知函数baxfx)(的图象经过点)3,1(,又其反函数)(1xf的图象经过点)0,2(,则函数)(xf的表达式是()A.12)(xxfB.22)(xxfC.32)(xxfD.42)(xxf10、已知向量a与b,则下列命题中正确的是()A.若|a|>|b|,则a>bB.若|a|=|b|,则a=bC.若a=b,则a∥bD.若ab,则a与b就不是共线向量11.下列函数中为偶函数的是()A.f(x)=1-x3B.f(x)=2x-1C.f(x)=x2+2D.f(x)=x312.一商场有三个大门,商场内有两部上楼的电梯,一顾客从商场外到商场二楼购物,不同的走法共有()A.5种B.6种C.8种D.9种第Ⅱ卷(非选择题共100分)二、填空题:(本大题共4小题,每小题4分,共16分.答案填在题中横线上)11.一个圆柱的底面半径和高都与一个球的直径相等,则该圆柱与该球的体积比为____________。12.若312sin,则cottan的值是____________。13.从0,1,2,3,4,5中任取3个数字,组成没有重复数字的三位数,其中能被5整除的三位数共有______________个.(用数字作答)14.已知nxx)(2121的展开式中各项系数的和是128,则展开式中x5的系数是.三、解答题:(本大题共7小题,共74分.解答应写出文字说明,证明过程或演算步骤)得分评卷人市姓名准考证号座位号2/415.(本小题满分12分)已知21)4tan((I)求tan的值;(II)求2cos1cos2sin2的值.16、某种消费品定价为每件60元,不征消费税时年销量为80万件,若政府征收消费税,当税率为x%,则销量减少x320万件,当x为何值时税金可取得最大?并求此最大值?(10分)17.(本小题满分8分)甲、乙两人向同一目标射击,他们击中目标的概率分别为21和31,求目标被击中的概率。18.(本小题满分14分)如图,在四棱锥ABCDP中,底面ABCD是正方形,侧棱PD底面ABCD,DCPD,E是PC的中点.(I)证明∥PA平面EDB;(II)求EB与底面ABCD所成的角的正切值.19.(本小题满分14分)已知数列}{na的前n项和2101nnSn。(1)求该数列的通项na;(2)求该数列所有正数项的和。20.(本小题满分16分)椭圆的中心是原点O,它的短轴长为22,相应于焦点)0)(0,(ccF的准线l与x轴相交于点A,||2||FAOF,过点A的直线与椭圆相交于P、Q两点.(I)求椭圆的方程及离心率;(II)若,0.OQOP求直线PQ的方程.对口高考模拟试卷数学试题参考解答一、选择题:本题考查基本知识和基本运算.每小题5分,满分50分.1.D2.A3.B4.A5.C6.A7.A8.B9.C10.C二、填空题:本题考查基本知识和基本运算.每小题4分,满分20分.11.8012.113.)413,(14.3615.35三、解答题16.本小题考查两角和正切公式,倍角的正弦、余弦公式等基础知识,考查运算能力.满分12分.解:(I)解:tan1tan1tan4tan1tan4tan)4tan(由21)4tan(,有21tan1tan1解得31tan⋯⋯⋯⋯⋯⋯⋯⋯4分(II)解法一:1cos21coscossin22cos1cos2sin222⋯⋯⋯⋯⋯⋯⋯⋯6分cos2cossin265213121tan⋯⋯⋯⋯⋯⋯⋯⋯12分解法二:由(I),31tan,得cos31sin22cos91sin22cos9...