勾股定理1（探究定理） (2)VIP免费

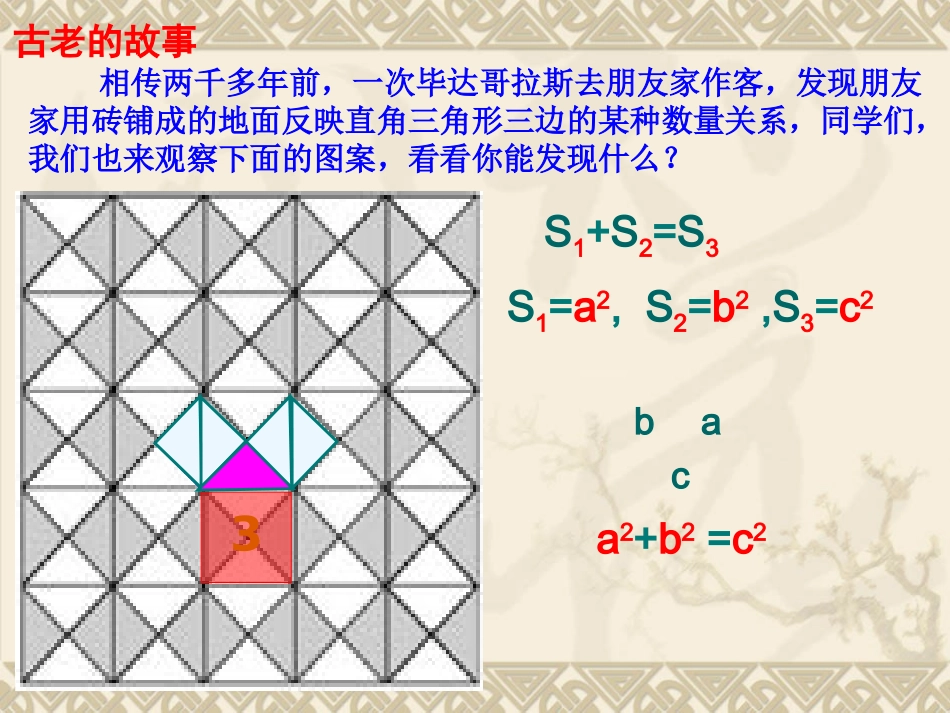
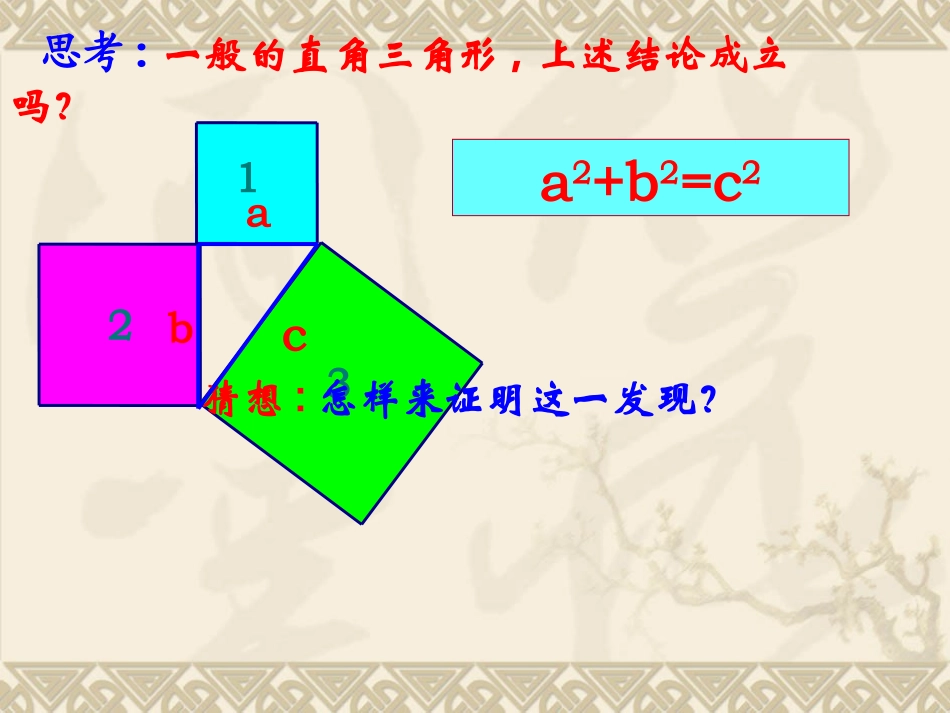
a2+b2=c2洪山嘴中学左仁东12相传两千多年前，一次毕达哥拉斯去朋友家作客，发现朋友家用砖铺成的地面反映直角三角形三边的某种数量关系，同学们，我们也来观察下面的图案，看看你能发现什么？3古老的故事S1+S2=S3abcS1=a2,S2=b2,S3=c2a2+b2=c2123acb思考:一般的直角三角形,上述结论成立吗？猜想:怎样来证明这一发现？a2+b2=c2abcabcbcabcaabc∴a²+b²=c²∴2ab+（b²-2ab+a²）=c²∵ab×4+(b-a)²=c²12∵4S△+S小正方形=S大正方形∴a²+b²=c²∴（a²+2ab+b²）-2ab=c²∵(a+b)²-ab×4=c²12∵S大正方形-4S△=S小正方形证法一：将四个全等的直角三角形拼成如图所示的内外各一个正方形证法二：（赵爽弦图）将四个全等的直角三角形拼成如图所示的内外各一个正方形美国第二十任总统伽菲尔德的证法在数学史上被传为佳话.为了纪念他对勾股定理直观、简捷、易懂、明了的“”证明，就把这一证法称为总统证法。证法三：总统证法abcabcABCD∵S△BCE=S梯形ABCD-2SABC△abbac212221221abbabac22221221abbabac221221221221221221bac222bac将两个全等的直角三角形拼成如图所示的直角梯形E┏a2+b2=c2acb直角三角形勾股弦人类最伟大的十个科学发现之一.两直角边的平方和等于斜边的平方.在中国古代，人们把弯曲成直角的手臂的上半部分称为"勾"，下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”，较长的直角边称为“股”，斜边称为“弦”.勾股勾股定理:(gou-gutheorem)外国人称：毕达哥拉斯定理满足三个整数,称为勾股数222abc如：32+42=52，你还能举一些常见的吗？⑴a2+b2＝c2abcABC在Rt△ABC中∠C=900⑶c2-a2=b2⑵c2-b2=a222bac勾股定理几种形式22bca22acb225B811.求下列图中字母所代表的图形的面积A3260cabS2536当堂练习一2.直角三角形的两边为6、8，求第三边当堂练习二125c4140a4600ab1根据下图中的数据求图中字母所表示的边长a2+b2=c2直角三角形两直角边的平方和等于斜边的平方.勾股定理：abc本节的学习内容⑴a2+b2＝c2⑶c2-a2=b2⑵c2-b2=a222bac22bca22acb勾股定理几种形式