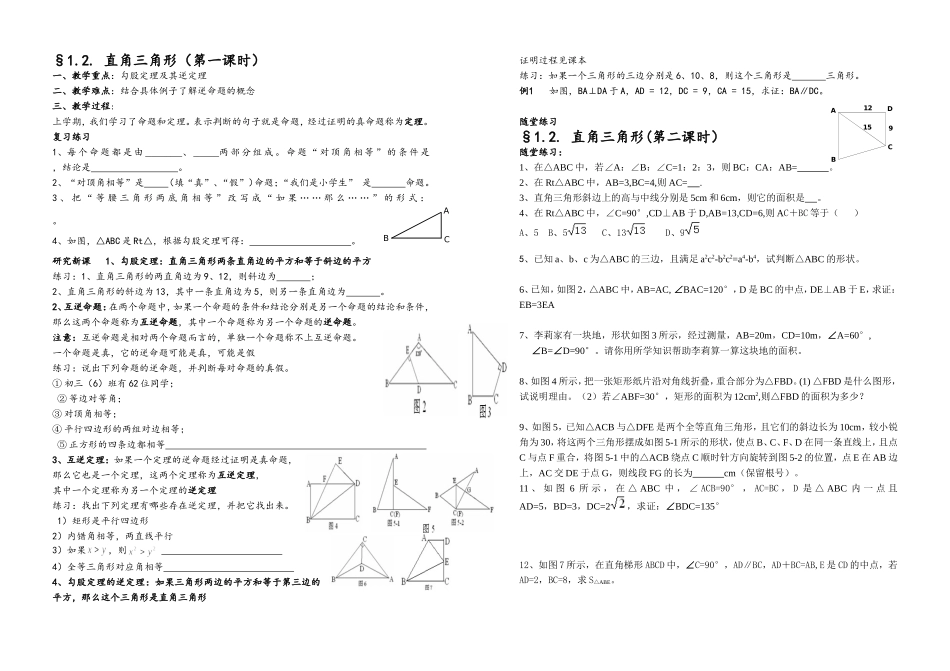
§1.2.直角三角形(第一课时)一、教学重点:勾股定理及其逆定理二、教学难点:结合具体例子了解逆命题的概念三、教学过程:上学期,我们学习了命题和定理。表示判断的句子就是命题,经过证明的真命题称为定理。复习练习1、每个命题都是由、两部分组成。命题“对顶角相等”的条件是,结论是。2、“对顶角相等”是(填“真”、“假”)命题;“我们是小学生”是命题。3、把“等腰三角形两底角相等”改写成“如果……那么……”的形式:。4、如图,△ABC是Rt△,根据勾股定理可得:。研究新课1、勾股定理:直角三角形两条直角边的平方和等于斜边的平方练习:1、直角三角形的两直角边为9、12,则斜边为;2、直角三角形的斜边为13,其中一条直角边为5,则另一条直角边为。2、互逆命题:在两个命题中,如果一个命题的条件和结论分别是另一个命题的结论和条件,那么这两个命题称为互逆命题,其中一个命题称为另一个命题的逆命题。注意:互逆命题是相对两个命题而言的,单独一个命题称不上互逆命题。一个命题是真,它的逆命题可能是真,可能是假练习:说出下列命题的逆命题,并判断每对命题的真假。①初三(6)班有62位同学;②等边对等角;③对顶角相等;④平行四边形的两组对边相等;⑤正方形的四条边都相等3、互逆定理:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理称为互逆定理,其中一个定理称为另一个定理的逆定理练习:找出下列定理有哪些存在逆定理,并把它找出来。1)矩形是平行四边形2)内错角相等,两直线平行3)如果,则4)全等三角形对应角相等4、勾股定理的逆定理:如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形证明过程见课本练习:如果一个三角形的三边分别是6、10、8,则这个三角形是三角形。例1如图,BA⊥DA于A,AD=12,DC=9,CA=15,求证:BA∥DC。随堂练习§1.2.直角三角形(第二课时)随堂练习:1、在△ABC中,若∠A:∠B:∠C=1:2:3,则BC:CA:AB=。2、在Rt△ABC中,AB=3,BC=4,则AC=.3、直角三角形斜边上的高与中线分别是5cm和6cm,则它的面积是。4、在Rt△ABC中,∠C=90°,CD⊥AB于D,AB=13,CD=6,则AC+BC等于()A、5B、5C、13D、95、已知a、b、c为△ABC的三边,且满足a2c2-b2c2=a4-b4,试判断△ABC的形状。6、已知,如图2,△ABC中,AB=AC,∠BAC=120°,D是BC的中点,DE⊥AB于E,求证:EB=3EA7、李莉家有一块地,形状如图3所示,经过测量,AB=20m,CD=10m,∠A=60°,∠B=∠D=90°。请你用所学知识帮助李莉算一算这块地的面积。8、如图4所示,把一张矩形纸片沿对角线折叠,重合部分为△FBD。(1)△FBD是什么图形,试说明理由。(2)若∠ABF=30°,矩形的面积为12cm2,则△FBD的面积为多少?9、如图5,已知△ACB与△DFE是两个全等直角三角形,且它们的斜边长为10cm,较小锐角为30,将这两个三角形摆成如图5-1所示的形状,使点B、C、F、D在同一条直线上,且点C与点F重合,将图5-1中的△ACB绕点C顺时针方向旋转到图5-2的位置,点E在AB边上,AC交DE于点G,则线段FG的长为cm(保留根号)。11、如图6所示,在△ABC中,∠ACB=90°,AC=BC,D是△ABC内一点且AD=5,BD=3,DC=2,求证:∠BDC=135°12、如图7所示,在直角梯形ABCD中,∠C=90°,AD∥BC,AD+BC=AB,E是CD的中点,若AD=2,BC=8,求S△ABE。DCBA12915ABC