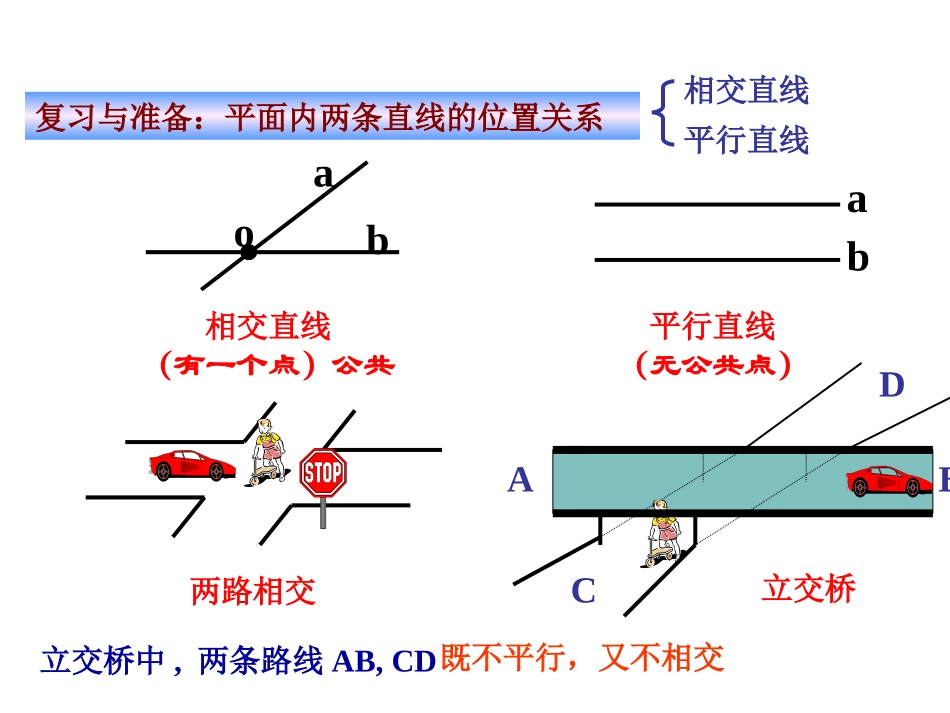
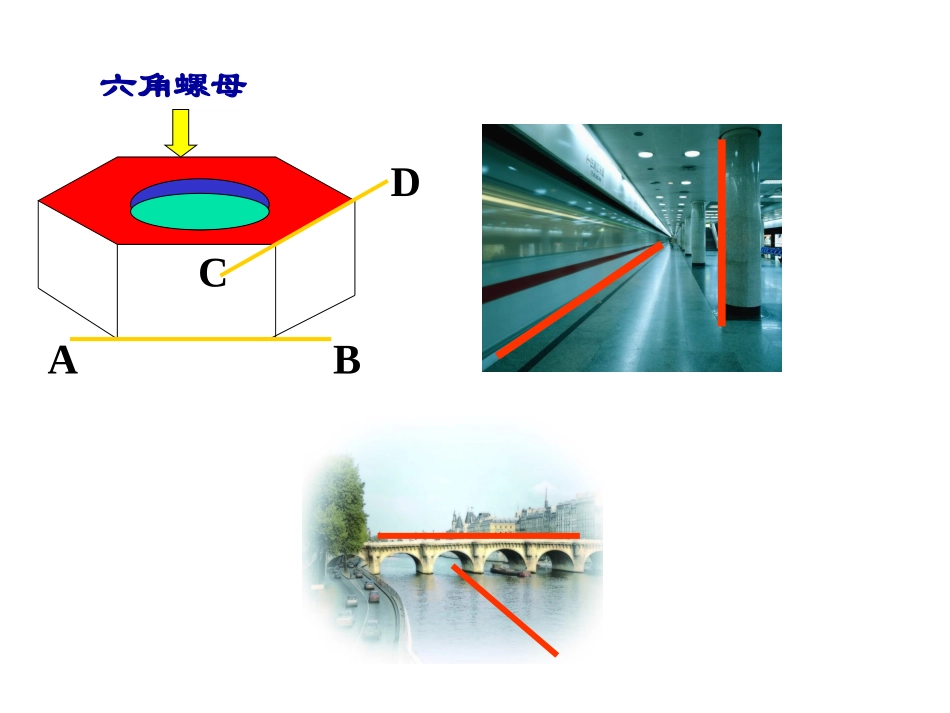
2.1.2空间中直线与直线之间的位置关系ABCD复习与准备:平面内两条直线的位置关系相交直线平行直线相交直线(有一个点)公共平行直线(无公共点)两路相交立交桥立交桥中,两条路线AB,CDaboab既不平行,又不相交ABCD六角螺母两直线异面的判别二:两条直线不同在任何一个平面内.两直线异面的判别一:两条直线既不相交、又不平行.注1不同在任何一个平面内的两条直线叫做异面直线。1.异面直线的定义:注意:在不同平面内的两条直线不一定异面a与b是相交直线a与b是平行直线a与b是异面直线abM答:不一定:它们可能异面,可能相交,也可能平行。分别在两个平面内的两条直线是否一定异面?abab合作探究一答案:D1C1、C1C、CD、D1D、AD、B1C1A1B1C1D1CBDA练习如图所示:正方体的棱所在的直线中,与直线A1B异面的有哪些?按平面基本性质分同在一个平面内相交直线平行直线不同在任何一个平面内:异面直线有一个公共点:按公共点个数分相交直线无公共点平行直线异面直线2.空间中直线与直线之间的位置关系3.异面直线的画法说明:画异面直线时,为了体现它们不共面的特点。常借助一个或两个平面来衬托.如图:aabaAbb(1)(3)(2)1.画两个相交平面,在这两个平面内各画一条直线,使它们成为:⑴平行直线;⑵相交直线;⑶异面直线.ab⑵巩固:ab⑴ab⑶2.两条异面直线指:()A.空间中不相交的两条直线;B.不在同一平面内的两条直线;C.不同在任一平面内的两条直线;D.分别在两个不同平面内的两条直线;E.空间没有公共点的两条直线;F.既不相交,又不平行的两条直线.巩固:合作探究二如图是一个正方体的展开图,如果将它还原为正方体,那么AB,CD,EF,GH这四条线段所在直线是异面直线的有对?FHCBEDGA答:共有三对GEHFD(C)A(B)abced我们知道,在同一平面内,如果两条直线都和第三条直线平行,那么这两条直线互相平行.在空间这一规律是否还成立呢?观察:将一张纸如图进行折叠,则各折痕及边a,b,c,d,e,…之间有何关系?a∥b∥c∥d∥e…∥公理4:在空间平行于同一条直线的两条直线互相平行.———平行线的传递性推广:在空间平行于一条已知直线的所有直线都互相平行.4.空间两直线平行的判定公理公理4平行于同一条直线的两直线互相平行.bac若a//b,c//b则a//c.下图长方体中平行相交异面②BD和FH是直线①EC和BH是直线③BH和DC是直线BACDEFHG(2).与棱AB所在直线异面的棱共有条?4分别是:CG、HD、GF、HE(1)说出以下各对线段的位置关系?5.例题选讲例1例2已知ABCD是四个顶点不在同一个平面内的空间四边形,E,F,G,H分别是AB,BC,CD,DA的中点,连结EF,FG,GH,HE,求证EFGH是一个平行四边形。解题思想: EH是△ABD的中位线∴EHFG∥且EH=FG∴EFGH是一个平行四边形证明:连结BD把所要解的立体几何问题转化为平面几何的问题——解立体几何时最主要、最常用的一种方法。ABDEFGHC∴EHBD∥且EH=BD21同理,FGBD∥且FG=BD21填空:1、空间两条不重合的直线的位置关系有________、________、________三种。2、没有公共点的两条直线可能是________直线,也有可能是________直线。3、和两条异面直线中的一条平行的直线与另一条的位置关系有______________。4、过已知直线上一点可以作______条直线与已知直线垂直。5、过已知直线外一点可以作______条直线与已知直线垂直。平行相交异面平行异面无数无数相交、异面1、分别在两个平面内的两条直线一定是异面直线。()2、空间两条不相交的直线一定是异面直线。()3、垂直于同一条直线的两条直线必平行。()4、若一条直线垂直于两条平行直线中的一条,则它一定与另一条直线垂直。()判断对错:思考题:1、a与b是异面直线,且ca∥,则c与b一定()。(A)异面(B)相交(C)平行(D)不平行2、正方体一条对角线与正方体的棱可组成的异面直线的对数是()对。(A)6(B)3(C)8(D)123、一条直线和两条异面直线都相交,则它们可以确定()平面。(A)一个(B)两个(C)三个(D)四个定理(等角定理):空间中,如果两个角的两边分别对应平行,那么这两个角相等或互补.观察:如图所示,长方体ABCD-A1B1C1D1中,ADC∠与∠A1D1C1,∠ADC与∠A1B1C1两边分别对...