二次函数y=ax2+bx+c的配方法(1)VIP免费

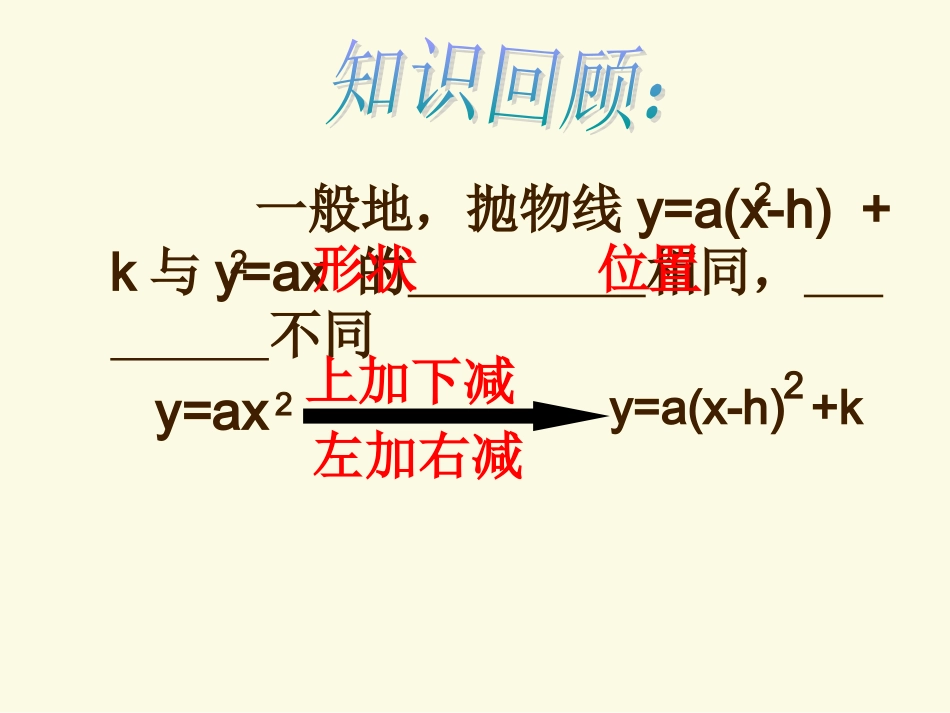
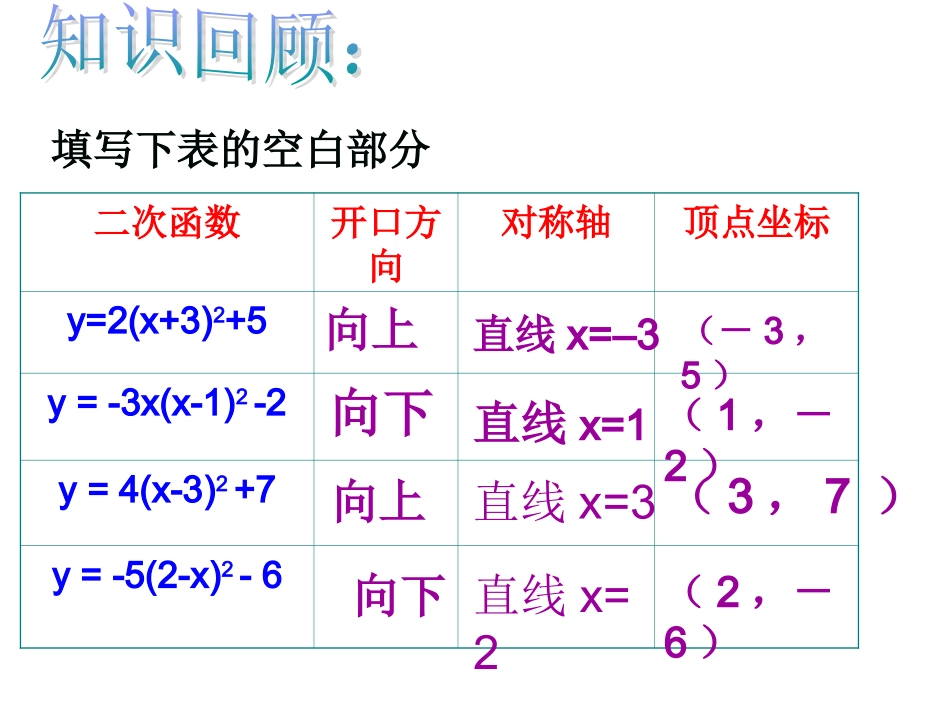
一般地，抛物线y=a(x-h)+k与y=ax的相同，不同22形状位置y=ax2y=a(x-h)+k2上加下减左加右减抛物线y=a(x-h)2+k有如下特点:1.当a0﹥时，开口，当a﹤0时，开口，向上向下2.对称轴是；3.顶点坐标是。直线X=h(h,k)二次函数开口方向对称轴顶点坐标y=2(x+3)2+5y=-3x(x-1)2-2y=4(x-3)2+7y=-5(2-x)2-6直线x=–3直线x=1直线x=2直线x=3向上向上向下向下（－3，5）（1，－2）（3，7）（2，－6）填写下表的空白部分我们知道,像y=a(x-h)2+k这样的函数,容易确定相应抛物线的顶点为(h,k),二次函数y=3x2-6x+5也能化成这样的形式吗?怎样把函数y=3x2-6x+5的转化成y=a(x-h）2+k的形式?函数y=ax²+bx+c的图象配方:5632xxy35232xx提取二次项系数3511232xx配方:加上再减去一次项系数一半的平方32132x整理:前三项化为平方形式，后两项合并同类项.2132x化简:去掉中括号老师提示:配方后的表达式通常称为顶点式简单说成：一提、二配、三化简函数y=3x2-6x+5的图象特征2.根据配方式(顶点式)确定开口方向,对称轴,顶点坐标. a=3>0,∴开口向上;对称轴:直线x=1;顶点坐标:(1,2)..2132xy吗？kh)a(xy改写成cbxaxy你能把22函数y=ax²+bx+c的顶点式配方:cbxaxy2ccxabxa2提取二次项系数acababxabxa22222配方:加上再减去一次项系数绝对值一半的平方222442abacabxa整理:前三项化为平方形式，后两项合并同类项.44222abacabxa化简:去掉中括号.44222abacabxay∴顶点坐标公式?二次函数y=ax²+bx+c的图象是一条抛物线..2:abx它的对称轴是直线.44,22abacab它的顶点是.44222abacabxay配方得：老师提示:这个结果通常称为顶点坐标公式.请你总结函数函数y=ax2+bx+c(a≠0)的图象和性质总结：二次函数y=ax2+bx+c的性质总结：二次函数y=ax2+bx+c的性质y=ax2+bx+c(a≠0)a>0a<0开口方向顶点坐标对称轴增减性极值向上向下在对称轴的左侧，y随着x的增大而减小。在对称轴的右侧，y随着x的增大而增大。在对称轴的左侧,y随着x的增大而增大。在对称轴的右侧，y随着x的增大而减小。x=-b2ax=-b2ay最小值=4ac-b24ax=-b2a(-,)b2a4ac-b24a(-,)b2a4ac-b24ay最大值=4ac-b24ax=-b2a抛线顶点标为.则22.物y=2x+bx+c的坐(-1,2),b=______，c=______441、写出下列抛物线的开口方向、对称轴及顶点坐标（P12练习）;23.12xxy;2.22xxy;882.32xxy.3421.42xxy?练习：(-1/3，-1/3)（-1,1）（2,0）（4，-5）B1.抛物线y=2x2+8x-11的顶点在（）A.第一象限B.第二象限C.第三象限D.第四象限2.不论k取任何实数，抛物线y=a(x+k)2+k(a≠0)的顶点都在A.直线y=x上B.直线y=-x上C.x轴上D.y轴上3.若二次函数y=ax2+4x+a-1的最小值是2,则a的值是A.4B.-1C.3D.4或-14.若二次函数y=ax2+bx+c的图象如下,与x轴的一个交点为(1,0),则下列各式中不成立的是()A.b2-4ac>0B.abc>0C.a+b+c=0D.a-b+c<01CAxyo-1B()（）5.若把抛物线y=x2+bx+c向左平移2个单位,再向上平移3个单位,得抛物线y=x2-2x+1,则A.b=2B.b=-6,c=6C.b=-8D.b=-8,c=186.若一次函数y=ax+b的图象经过第二、三、四象限，则二次函数y=ax2+bx-3的大致图象是()()BxyoxyoxyoxyoABCD-3-3-3-3C7.在同一直角坐标系中,二次函数y=ax2+bx+c与一次函数y=ax+c的大致图象可能是（）CxyoxyoxyoxyoABCD1432xxy322xxy例1.说出下列函数的开口方向、对称轴、顶点坐标，最值，增减性：指出抛物线:254yxx的开口方向，求出它的对称轴、顶点坐标、与y轴的交点坐标、与x轴的交点坐标，最值以及增减性。练习①y=2x2-5x+3③y=(x-3)(x+2)②y=－x2+4x-9例2.求下列二次函数图像的开口、顶点、对称轴，并画出草图：21请画出草图:3－9－61、当x取何值时，二次函数有最大值或最小值，最大值或最小值是多少？2281yxx学以致用2、已知函数当x为何值时，函数值y随自变量的值的增...