空间向量在立体几何中的应用（高三二轮复习VIP免费

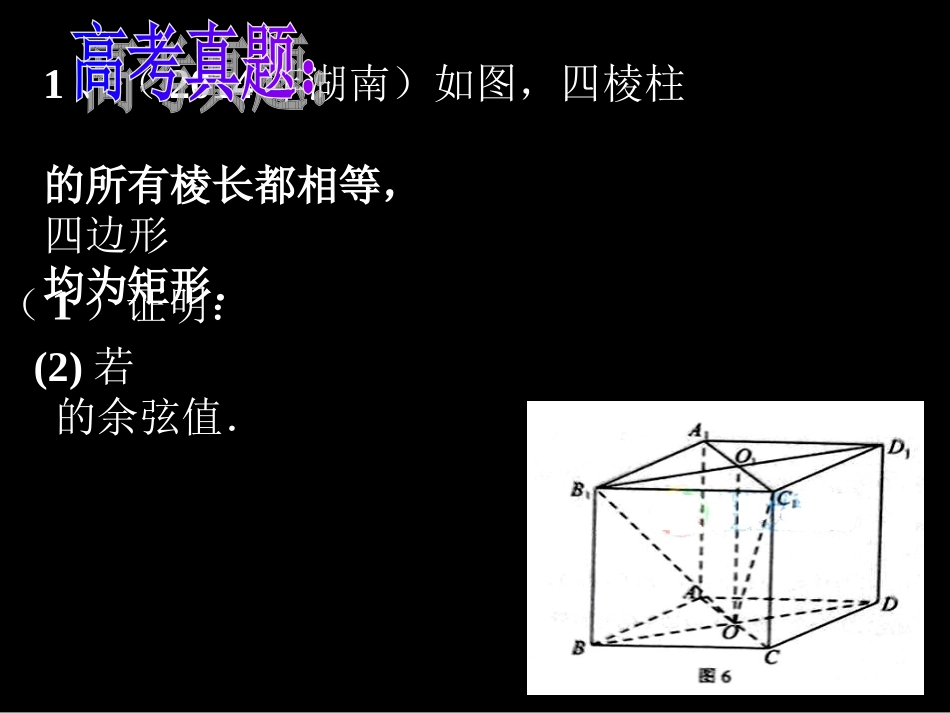
高三二轮专题复习授课人：彭信军1．考题展望:空间向量及应用是立体立体几的重点考查内容，常常以解答题中一问形式考查角或距离的计算，大多可以用传统几何法和用空间向量求解，而且更侧重于后者，并有拓展为存在性、探索性题型趋势，解答时大多体现函数与方程思想．1111ABCDABCD11111,,ACBDOACBDO1111ACCABDDB和四边形1、（2014年湖南）如图，四棱柱的所有棱长都相等，四边形均为矩形．（1）证明：1;OOABCD底面1160,CBACOBD求二面角(2)若的余弦值．3月26日共收作业22人习题正确人数不全对人数错误人数2014年湖南8131基础练习11606基础练习21705基础练习301482012年江西2614巩固练习11183巩固练习2没做完没做完没做完…………..4分（1）证明：∵四边形ABCD与四边形A1B1C1D1均为菱形∴点O,O1为AC与A1C1中点则OO1//CC1又∵四边形ACC1A1为矩形则CC1AC⊥∴OO1AC⊥同理OO1BD⊥又∵AC∩BD=O∴OO1⊥面ABCDxyz11OBC，，，)0,1,0()2,1,0(),2,0,3(),0,0,0(1,3602.,,)2(111101nBBDDCBOOCOBCBAABxyzOzyxOOOCOBO的法向量为面则各点坐标为，，设系轴，建立空间直角坐标轴，轴，所在直线分别为为坐标原点，以………..6分xyz11OBC，，195721932||||||cos)3,32,2(32,23212111202302112{nnnnDOBCnyxzOBCnzxzy为锐角则的角由图象可知二面角，所以，则取则的一个法向量，是面设……10分…………12分3月26日共收作业22人习题正确人数不全对人数错误人数2014年湖南8131基础练习11606基础练习21705基础练习301482012年江西2614巩固练习11183巩固练习2没做完没做完没做完1、基础练习：(1)空间两异面直线AB与CD的对应的向量是，则异面直线AB与CD夹角的余弦值为______)2,1,1()1,0,1(CDAB与)1,0,1(MN)0,1,1(n的法向量为面(2)空间一直线MN所得的向量为，则直线MN与面所成的角为__________，(3)在平行四边形ABCD中，AB＝AC＝1，∠ACD＝90°，将它沿对角线AC折起，使AB与CD成60°角，则D、B间的距离是__________．2或230063ba,(1)异面直线夹角：设两条异面直线a，b的方向向量为,则cos＝________(其中为异面直线a，b所成的角)．en(2)线面角：设直线l的方向向量为，平面α的法向量为，直线l与平面α所成的角为，则有sin＝_________.||||||baba为线与法向量的夹角）(|||||||cos|nene21,nn(3)二面角：分别是二面角αlβ的两个半平面α，β的法向量，则二面角的大小θ＝．(4)点到面的距离：空间点P与面α中任一点A所得向量为,面α的法向量为则点P到面α的距离d=___________________PAn||||nnPA2121,,nnnn或511ABC2、典例分析1（2012年江西）在三棱柱ABC-A1B1C1中，已知AB=AC=AA1=，BC=4，在A1在底面ABC的投影是线段BC的中点O。（1）证明在侧棱AA1上存在一点E，使得OE⊥平面BB1C1C，并求出AE的长；（2）求平面与平面BB1C1C夹角的余弦值。xyz补充：求三棱锥B1-AOA1的体积3、巩固练习本节课我们主要学习了：1、用空间向量解决立体几何的的求角、线上点的问题；2、用空间向量解决立体几何问题要求要有空间想象能力和准确的运算能力