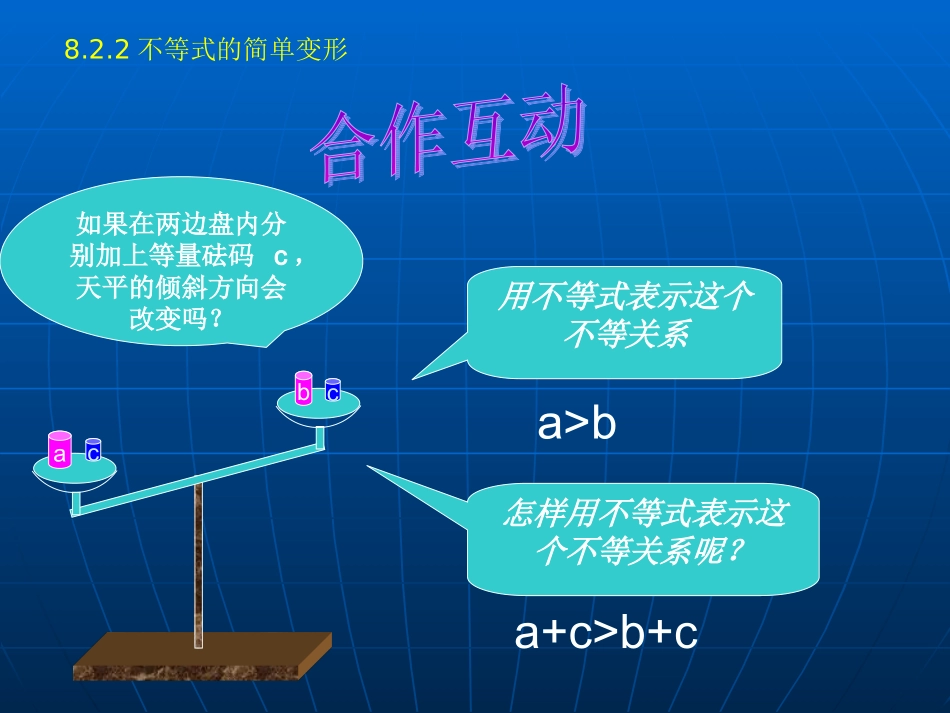
8.2.28.2.2不等式的简单变形不等式的简单变形等式的两边都加上(或减去)同一个数或同等式的两边都加上(或减去)同一个数或同一个整式,所得结果仍是等式。一个整式,所得结果仍是等式。如果如果a=b,a=b,那么那么a+c=b+c,a-c=b-ca+c=b+c,a-c=b-c..等式的两边都乘以(或除以)同一个数(除数等式的两边都乘以(或除以)同一个数(除数不能为不能为00),所得结果仍是等式。),所得结果仍是等式。如果如果a=b,a=b,那么那么ac=bc,ac=bc,((c≠0c≠0))..cbca等式的性质一等式的性质二8.2.2不等式的简单变形abcc用不等式表示这个不等关系a>b怎样用不等式表示这个不等关系呢?a+c>b+c如果在两边盘内分别加上等量砝码c,天平的倾斜方向会改变吗?8.2.2不等式的简单变形导纲一:根据上述实验你能发现不导纲一:根据上述实验你能发现不等式的什么变形规律?等式的什么变形规律?不等式的基本性质不等式的基本性质11如果如果a>b,a>b,那么那么a+c>b+c,a+c>b+c,a-c>b-c.a-c>b-c.不等式的两边都加上(或减去)同一个数不等式的两边都加上(或减去)同一个数或同一个整式,不等号的方向不变。或同一个整式,不等号的方向不变。8.2.2不等式的简单变形不等式两边都乘以(或除以)同一个不为零的数,不等号的方向是否发生改变?8.2.2不等式的简单变形导纲二:在不等式7>4的两边都乘以(或除以)同一个正数、负数、零,不等号的方向会发生什么变化?7×3_______4×3,7×2_______4×2,7×1_______4×1,7×0_______4×0,7×(-1)_______4×(-1),7×(-2)_______4×(-2),7×(-3)_______4×(-3),………………………………………………>>>=<<<从中你能发现什么规律?8.2.2不等式的简单变形不变改变不等式的性质2:如果a>b,并且c>0,那么ac>bc,.不等式两边都乘以(或除以)同一个正数,不等号的方向不变。不等式的性质3:如果a>b,并且c<0,那么ac-3(2)-2x<6解:不等式的两边都乘以,不等号的方向,所以12x×2>-3×2-2x×12(-)<6×12(-)x>-6x<-3导纲四:这里的变形,与方程变形中的()类似,它的依据是什么?未知数的系数化为1依据是不等式的性质2或3注意:根据不等式两边乘以(或除以)的数是正数还是负数,来确定变形时不等号的方向是否需要改变。解:不等式的两边都乘以,不等号的方向,所以>>8.2.2不等式的简单变形2不变21_改变11、下面各题的结论对吗?请说出你的理由:、下面各题的结论对吗?请说出你的理由:(1)(1)如果如果a+8a+8>>44,那么,那么aa>>-4-4;();()(2)(2)如果如果4a4a>>4b4b,那么,那么aa>>bb;();()(3)(3)如果如果aa>>bb,那么,那么-3a+5-3a+5>>-3b+5-3b+5;;()()2、解不等式(1)3X-2>7.(2)4X+1>3X-2.(3)6X<8X-5.(4)-8X≤103、每个同学结合本节课所学内容编一道题,并在组内互相解答.拓展训练8.2.2不等式的简单变形导学归纳:导学归纳:通过本节课的学习,谈谈大家的收获:通过本节课的学习,谈谈大家的收获:11、在知识上有哪些收获?、在知识上有哪些收获?22、在数学思想,方法上有哪些收获?、在数学思想,方法上有哪些收获?8.2.2不等式的简单变形(1)掌握了不等式的三个性质.(2)应用不等式的性质对不等式进行简单变形.(3)知道了解不等式与解方程的异同之处.(1)体会了类比的数学思想.(2)掌握了从特殊到一般的数学方法.你还存在哪些疑惑?布置作业:书本58页练习题1,2,3,4.