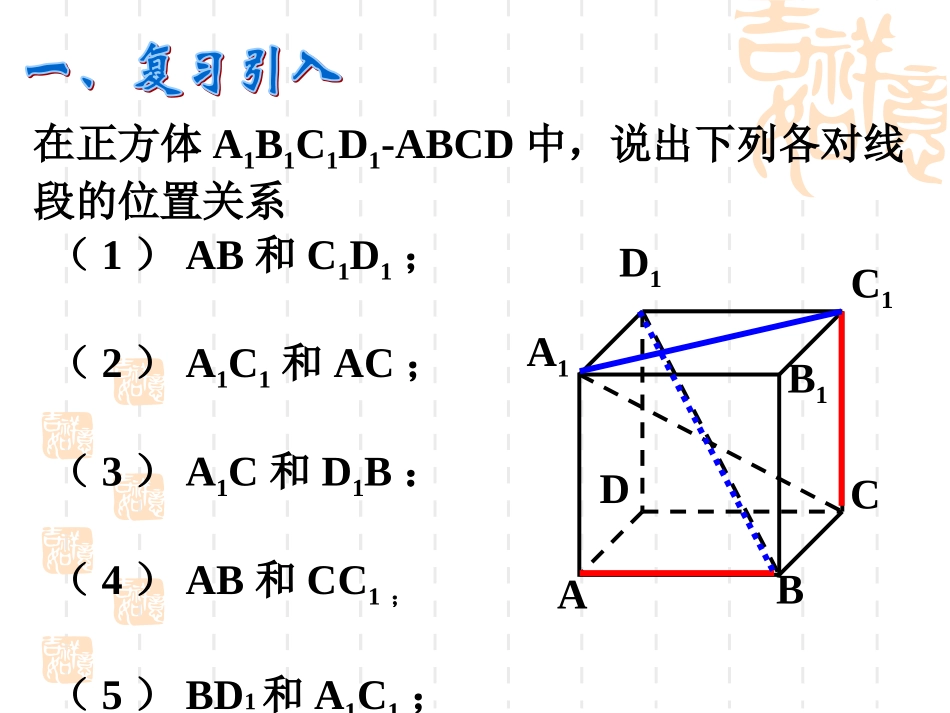
2.1.2空间中直线与直线之间的位置关系(1)问题:平面几何中,两条直线的位置关系:平行或相交在空间中是否还是如此呢?在正方体A1B1C1D1-ABCD中,说出下列各对线段的位置关系ABCDA1B1C1D1(1)AB和C1D1;(2)A1C1和AC;(3)A1C和D1B:(4)AB和CC1;(5)BD1和A1C1;异面直线:不同在任何一个平面内的两条直线。(即既不平行也不相交)异面直线的画法:αabαabbaαAa空间两条直线的位置关系1、平行ab没有公共点2、相交bAαa3、异面没有公共点b只有一个公共点Aba练习:判断下列说法的对错1、分别在两个平面内的两条直线一定是异面直线;3、a与b是异面直线,b与c是异面直线,则a与c是异面直线;4、a与b是共面,b与c是共面,则a与c共面一定异面;、则、baba,,2FFFF练习2:正方体ABCD-A1B1C1D1ABCDA1B1C1D11、与A1A是异面的有:2、与D1B异面的有:BCDCB1C1D1C1AA1ADA1B1B1C1CC1CDP50探究三、平行直线的传递性公理4平行同一条直线的两条直线互相平行.设设aa,,bb,,cc为直线为直线a∥bc∥ba∥caabbccaa,,bb,,cc三条直线两两平行,可以记为a∥b∥c符号语言(空间平行线的传递性)思考1:在平面上,如果一个角的两边与另一个角的两边分别平行,那么这两个角的大小有什么关系?四、等角定理思考2:如图,四棱柱ABCD--A′B′C′D′的底面是平行四边形,∠ADC与∠A′D′C′,∠ADC与∠B′A′D′的两边分别对应平行,这两组角的大小关系如何?BADCA'B'D'C'BADCA'B'D'C'等角定理空间中如果两个角的两边分别对应平行,那么这两个角相等或互补.例1如图是一个正方体的表面展开图,如果将它还原为正方体,那么AB,CD,EF,GH这四条线段所在直线是异面直线的有多少对?FAHGEDCBCDBAEFGH例2如图,空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点.(1)求证:四边形EFGH是平行四边形.(2)若AC=BD,那么四边形EFGH是什么图形?FGDAEBCH思考:若再加上条件AC=BD,那么四边形EFGH是什么图形?aα五、异面直线所成角的定义:1.直线a、b是异面直线。经过空间任意一点O,分别作直线a1a∥,b1b∥。我们把直线a1和b1所成的锐角(或直角)叫做异面直线a和b所成的角。ba1b1ObaαOθ为了简便,点O常取在两条异面直线中的一条上。o9002.异面直线a和b所成的角的范围:a1如果两条异面直线所成的角是直角,就说这两条异面直线互相垂直。相交垂直(有垂足)垂直异面垂直(无垂足)OααO因此,异面直线所成角的范围是(0,]3、特例:2例3.如图,在正方体中,(1)哪些棱所在的直线与直线BA1成异面直线?(2)求直线BA1和CC1所成的角的大小。(3)哪些棱所在的直线与直线A1A垂直。ABCDA1B1C1D1例题分析:解:(1)与直线BA1成异面直线有AD、CD、B1C1、C1D1、C1C、D1D(2) B1BC∥1C∴∠A1BB1是异面直线BA1和CC1所成的角易求得所成的角为45求求异面直线所成的角的一般步骤的一般步骤是是::根据异面直线所成角的定义,求异面直线所成角,就是要将其变换成相交直线所成有角。其方法为:平移法:即根据定义,以“运动”的观点,用“平移转化”的方法,使之成为相交直线所成的角。(1)(1)找出或作出有关的图形;找出或作出有关的图形;(2)(2)证明它符合定义;证明它符合定义;(3)(3)计算。计算。[[即:要求先证,要证先即:要求先证,要证先作。作。]]1、一条直线与两条异面直线中的一条相交,那么它与另一条之间的位置关系是()A、平行B、相交C、异面D、可能平行、可能相交、可能异面2、两条异面直线指的是()A、没有公共点的两条直线B、分别位于两个不同平面的两条直线C、某一平面内的一条直线和这个平面外的一条直线D、不同在任何一个平面内的两条直线练习:DD3、两条直线不相交是这两条直线异面的条件_______.4、两条直线不平行是这两条直线异面的条件5、下列命题中,其中正确的是(1)若两条直线没有公共点,则这两条直线互相平行(2)若两条直线都和第三条直线相交,那么这两条直线互相平行(3)若两条直线都和第三条直线平行,那么这两条直线互相平行(4)若两条直线都和第三条直线异面,那么这两条直线互相平行6、三个平面两两相交,所得的三条交线()A、交于一点...